拓扑排序算法(Java实现)
由 AOV 网可以得到拓扑排序。在介绍拓扑排序之前,先来介绍一下 AOV 网。
在 AOV 网中,若从顶点 vi 到顶点 vj 之间存在一条路径,则顶点 vi 是顶点 vj 的前驱,顶点 vj 为顶点 vi 的后继。若 <vi,vj>是有向网的一条弧,则称顶点 vi 是顶点 vj 的直接前驱,顶点 vj 是顶点 vi 的直接后继。
活动中的制约关系可以通过 AOV 网中的弧表示。例如,计算机科学与技术专业的学生必须修完一系列专业基础课程和专业课程才能毕业,学习这些课程的过程可以被看成是一个工程,每一门课程可以被看成是一个活动。计算机科学与技术专业的基本课程及选修课程的关系如下表所示。
在这些课程中,《高等数学》是基础课,它独立于其他课程。在修完《程序设计语言》和《离散数学》后,才能学习《数据结构》。这些课程构成的有向无环图如下图所示。
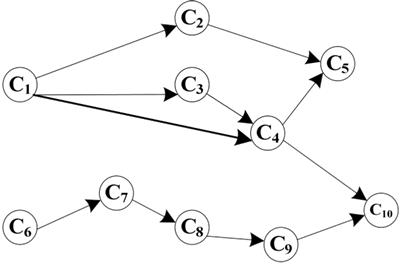
图 1 表示课程之间优先关系的有向无环图
在 AOV 网中,不允许出现环,如果出现环,就表示某个活动是自己的先决条件。因此,需要对 AOV 网判断是否存在环,可以利用有向图的拓扑排序进行判断。
对 AOV 网进行拓扑排序的方法如下:
按照以上步骤,图 2 所示的 AOV 网的拓扑序列为:(C1, C2, C3, C4, C5, C6, C7, C8, C9, C10) 或 (C6, C7, C8, C9, C1, C2, C3, C4, C5, C10)。
AOV 网的拓扑序列的构造过程如下图所示:
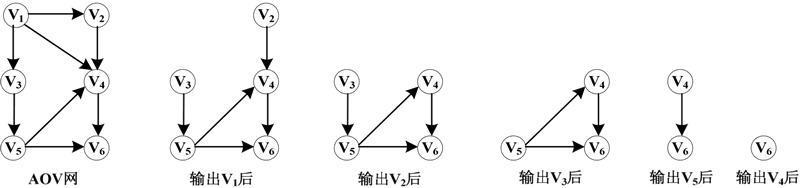
图 2 AOV网构造拓扑序列的过程
拓扑序列为:V1、V2、V3、V5、V4、V6。
在对 AOV 网进行拓扑排序结束后,可能会出现两种情况:
采用邻接表存储结构的 AOV 网的拓扑排序的算法实现:
AOV 网的拓扑排序算法如下:
AOV网
在每个工程中,可以将一个工程分为若干子工程,这些子工程称为活动。如果用图中的顶点表示活动,以有向图的弧表示活动之间的优先关系,这样的有向图称为 AOV 网,即顶点表示活动的网。在 AOV 网中,若从顶点 vi 到顶点 vj 之间存在一条路径,则顶点 vi 是顶点 vj 的前驱,顶点 vj 为顶点 vi 的后继。若 <vi,vj>是有向网的一条弧,则称顶点 vi 是顶点 vj 的直接前驱,顶点 vj 是顶点 vi 的直接后继。
活动中的制约关系可以通过 AOV 网中的弧表示。例如,计算机科学与技术专业的学生必须修完一系列专业基础课程和专业课程才能毕业,学习这些课程的过程可以被看成是一个工程,每一门课程可以被看成是一个活动。计算机科学与技术专业的基本课程及选修课程的关系如下表所示。
| 课程编号 | 课程名称 | 选修课程编号 |
|---|---|---|
| C1 | 程序设计语言 | 无 |
| C2 | 汇编语言 | C1 |
| C3 | 离散数学 | C1 |
| C4 | 数据结构 | C1,C3 |
| C5 | 编译原理 | C2,C4 |
| C6 | 高等数学 | 无 |
| C7 | 大学物理 | C6 |
| C8 | 数字电路 | C7 |
| C9 | 计算机组成结构 | C8 |
| C10 | 操作系统 | C9 |
在这些课程中,《高等数学》是基础课,它独立于其他课程。在修完《程序设计语言》和《离散数学》后,才能学习《数据结构》。这些课程构成的有向无环图如下图所示。

图 1 表示课程之间优先关系的有向无环图
在 AOV 网中,不允许出现环,如果出现环,就表示某个活动是自己的先决条件。因此,需要对 AOV 网判断是否存在环,可以利用有向图的拓扑排序进行判断。
拓扑排序
拓扑排序就是将 AOV 网中的所有顶点排列成一个线性序列,并且序列满足以下条件:在 AOV 网中,若从顶点 vi 到 vj 存在一条路径,则在该线性序列中,顶点 vi 一定出现在顶点 vj 之前。
因此,拓扑排序的过程就是将 AOV 网排成线性序列的操作。AOV 网表示一个工程图,而拓扑排序则是将 AOV 网中的各个活动组成一个可行的实施方案。对 AOV 网进行拓扑排序的方法如下:
- 在 AOV 网中任意选择一个没有前驱的顶点,即顶点入度为零,将该顶点输出。
- 从 AOV 网中删除该顶点,以及从该顶点出发的弧。
- 重复执行步骤 1 和步骤 2,直到 AOV 网中所有顶点都已经被输出,或者 AOV 网中不存在无前驱的顶点为止。
按照以上步骤,图 2 所示的 AOV 网的拓扑序列为:(C1, C2, C3, C4, C5, C6, C7, C8, C9, C10) 或 (C6, C7, C8, C9, C1, C2, C3, C4, C5, C10)。
AOV 网的拓扑序列的构造过程如下图所示:

图 2 AOV网构造拓扑序列的过程
拓扑序列为:V1、V2、V3、V5、V4、V6。
在对 AOV 网进行拓扑排序结束后,可能会出现两种情况:
- 一种是 AOV 网中的顶点全部输出,表示网中不存在回路;
- 另一种是 AOV 网中还存在没有输出的顶点,未输出顶点的入度都不为零,表示网中存在回路。
采用邻接表存储结构的 AOV 网的拓扑排序的算法实现:
- 遍历邻接表,将各个顶点的入度保存在数组 indegree 中。将入度为零的顶点入栈;
- 依次将栈顶元素出栈并输出该顶点,对该顶点的邻接顶点的入度减 1,若邻接顶点的入度为零,则入栈,否则,将下一个邻接顶点的入度减 1 并进行相同的处理;
- 继续将栈中的元素出栈,重复执行以上操作,直到栈空为止。
AOV 网的拓扑排序算法如下:
public int TopologicalOrder(AdjGraph G) throws Exception
// 采用邻接表存储结构的有向图 G 的拓扑排序
{
int count = 0;
int[] indegree = new int[G.vexnum]; // 数组 indegree 存储各顶点的入度
// 将图中各顶点的入度保存在数组 indegree 中
for (int i = 0; i < G.vexnum; i++) // 为数组 indegree 赋初值
{
indegree[i] = 0;
}
for (int i = 0; i < G.vexnum; i++) {
ArcNode p = G.vertex[i].firstarc;
while (p != null) {
int k = p.adjvex;
indegree[k] += 1;
p = p.nextarc;
}
}
SeqStack<Integer> S = new SeqStack<Integer>();
System.out.println("拓扑序列: ");
for (int i = 0; i < G.vexnum; i++) {
if (indegree[i] == 0) // 将入度为零的顶点入栈
S.PushStack(i);
}
while (!S.StackEmpty()) // 如果栈 S 不为空
{
int i = S.PopStack(); // 从栈 S 将已拓扑排序的顶点 i 弹出
System.out.print(G.vertex[i].data + " ");
count += 1; // 对入栈 T 的顶点计数
ArcNode p = G.vertex[i].firstarc;
while (p != null) {
int k = p.adjvex;
indegree[k] -= 1;
if (indegree[k] == 0) // 若 k 的入度减 1 后变为 0,则将 k 入栈 S
S.PushStack(k);
p = p.nextarc;
}
}
if (count < G.vexnum) {
System.out.println("该有向网有回路");
return 0;
} else
return 1;
}
在拓扑排序的实现过程中,入度为零的顶点入栈的时间复杂度为 O(n),有向图的顶点入栈、出栈操作及 while 循环语句的执行次数是 e,因此,拓扑排序的时间复杂度为 O(n+e)。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: