二叉搜索树(BST)详解(图文并茂,C++实现)
在线性表中进行顺序查找和二分查找,在最坏情况和平均情况下的时间复杂度分别为 O(n) 和 O(logn)。但进行二分查找的前提是线性表必须有序,若无序,则无法进行二分查找。
顺序查找和二分查找都适用于静态查找,若在查找过程中有插入、删除等修改操作,则在最坏情况和平均情况下的时间复杂度都为 O(n)。
是否存在一种数据结构和算法,既可以高效地查找,又可以高效地动态修改?实际上,将二分查找与二叉树结合起来,可以实现二叉搜索树结构,达到单次修改和查找的时间复杂度均为 O(logn)。
二叉搜索树(Binary Search Tree,BST),又叫作“二叉查找树”“二叉排序树”,是一种对查找和排序都有用的特殊的二叉树。
二叉搜索树或是空树,或是满足如下性质的二叉树:
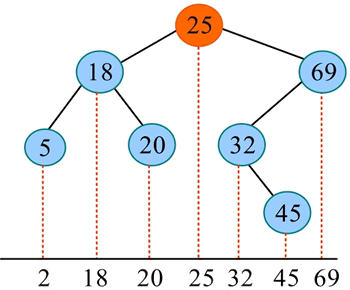
二叉搜索树的特性:左子树<根<右子树。二叉搜索树的中序遍历序列是一个递增序列。例如,一棵二叉搜索树,其中序遍历序列如下图所示。
算法步骤:
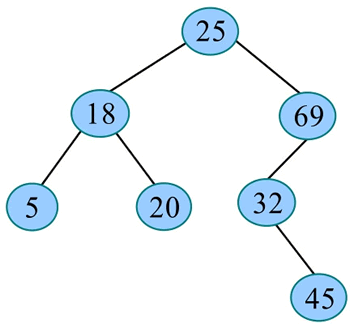
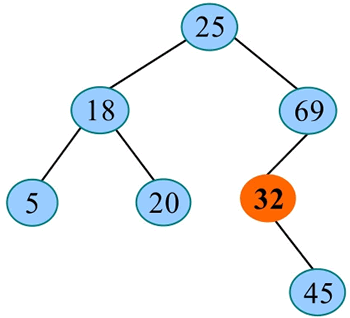
例如,一棵二叉搜索树如下图所示,查找关键字 32:
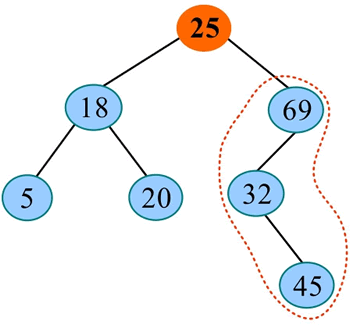
1) 将 32 与二叉搜索树的根 25 进行比较,32>25,在右子树中查找:
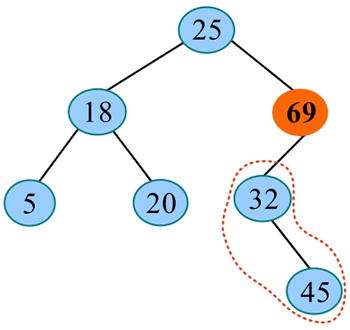
2) 将 32 与右子树的根 69 进行比较,32<69,在左子树中查找:
3) 将 32 与左子树的根 32 进行比较,相等,查找成功:
二叉搜索树查找算法实现:
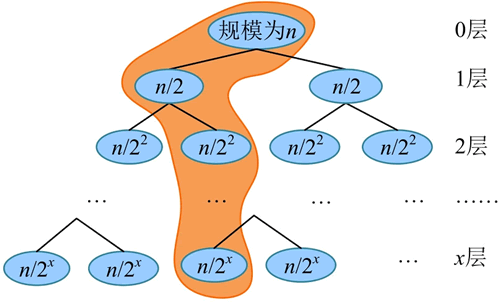
1) 在最好情况下,二叉搜索树与二分查找的判定树形态相似,如下图所示。每次查找范围都可以缩小一半,查找路径最多从根到叶子,比较次数最多为树的高度 logn,在最好情况下进行查找操作的时间复杂度为 O(logn)。
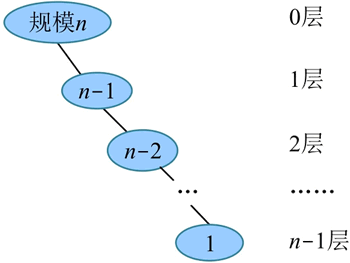
2) 在最坏情况下,二叉搜索树为单支树,只有左子树或右子树,如下图所示。每次查找范围都缩小为 n-1 个元素,退化为顺序查找,在最坏情况下进行查找操作的时间复杂度为 O(n)。
3) 在平均情况下,有 n 个节点的二叉搜索树有 Cn 棵(Cn 为卡特兰数),可以证明,在平均情况下进行查找操作的时间复杂度也为 O(logn)。
算法步骤:
例如,一棵二叉搜索树如下图所示,向其中插入关键字 30。
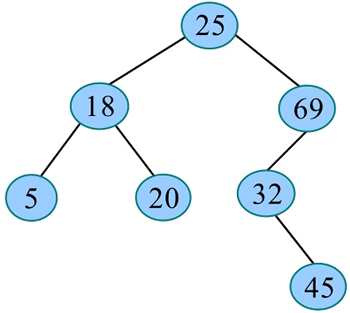
1) 将 30 与根 25 进行比较,30>25,在 25 的右子树中查找:
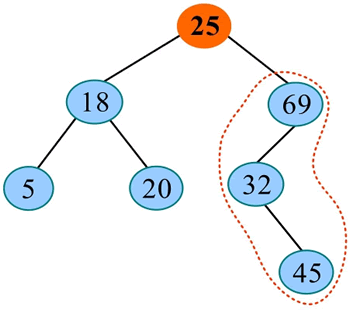
2) 将 30 与右子树的根 69 进行比较,30<69,在 69 的左子树中查找:
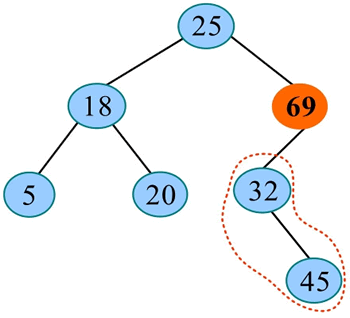
3) 将 30 与左子树的根 32 进行比较,30<32,在 32 的左子树中查找:
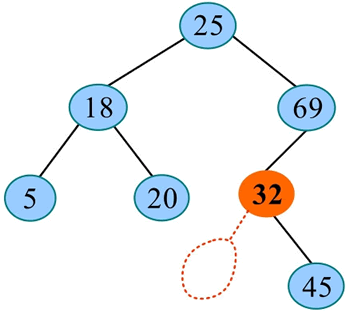
4) 32 的左子树为空,将 30 作为新叶子插入 32 的左子树:
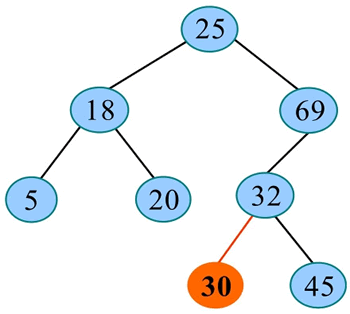
二叉搜索树插入算法实现:
算法实现:
实质上,创建二叉搜索树与快速排序一样,根相当于快速排序中的基准元素,左、右部分的划分情况取决于基准元素。输入序列的次序不同,创建的二叉搜索树也不同。
假设指针 p 指向待删除节点,指针 f 指向 p 的双亲。根据待删除节点所在位置的不同,具体的删除操作也不同,可分为下面三种情况。
1) 被删除节点的左子树为空。若被删除节点的左子树为空,则令其右子树“子承父业”代替其位置即可。例如,在二叉搜索树中删除 P,如下图所示。
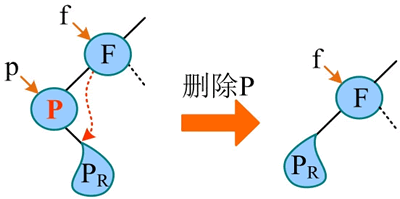
2) 被删除节点的右子树为空。若被删除节点的右子树为空,则令其左子树“子承父业”代替其位置即可,如下图所示。
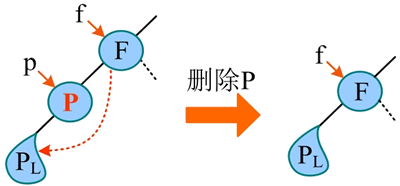
3) 被删除节点的左、右子树均不为空。若被删除节点的左子树和右子树均不为空,则无法再“子承父业”了。
根据二叉搜索树的中序遍历有序性,删除该节点时,可以首先用其直接前驱(或直接后继)代替其位置,然后删除其直接前驱(或直接后继)即可。
那么,在中序遍历序列中,一个节点的直接前驱(或直接后继)是哪个节点呢?
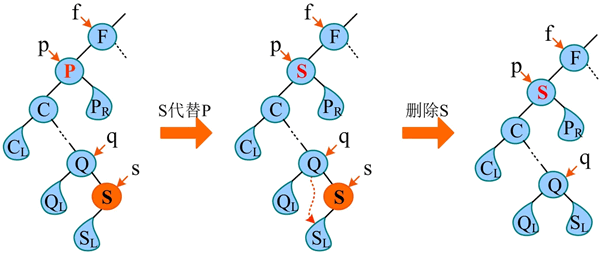
以 P 的直接前驱 S 代替 P,之后删除 S 即可。S 为最右节点,没有右子树,删除 S 后,左子树“子承父业”代替 S,如下图所示。
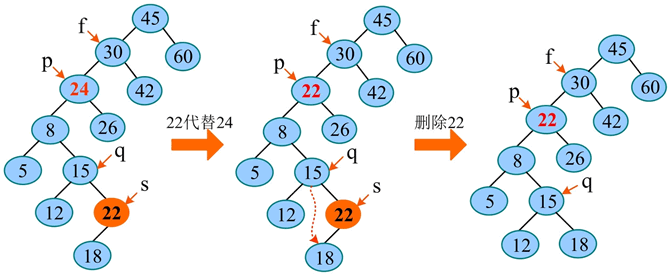
例如,在二叉搜索树中删除 24。首先找到 24 的位置 p,然后找到 p 的直接前驱 22,把 22 代替 24,删除 22,删除过程如下图所示。
删除节点之后是不是仍然满足二叉搜索树的中序遍历有序性?
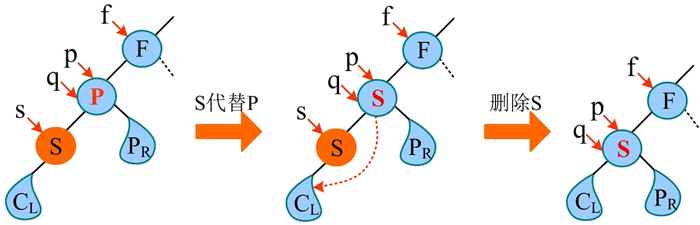
需要注意的是,有一种特殊情况:如下图所示,P 的左孩子没有右子树,S 就是其左子树的最右节点(直接前驱),则首先用 S 代替 P,然后删除 S 即可。S 为最右节点且没有右子树,删除 S 后,左子树“子承父业”代替 S。
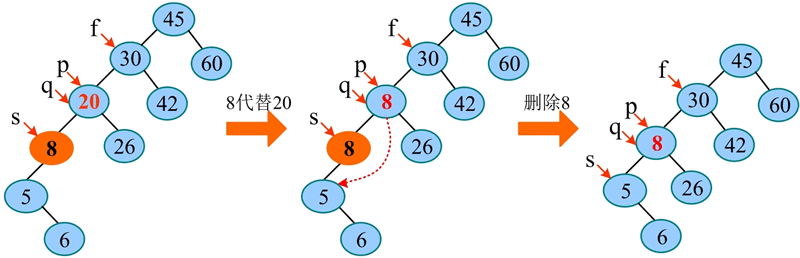
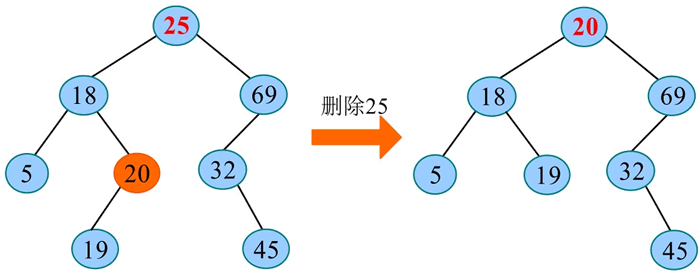
例如,在二叉搜索树中删除 20,删除过程如下图所示。
二叉搜索树删除元素的算法步骤如下:
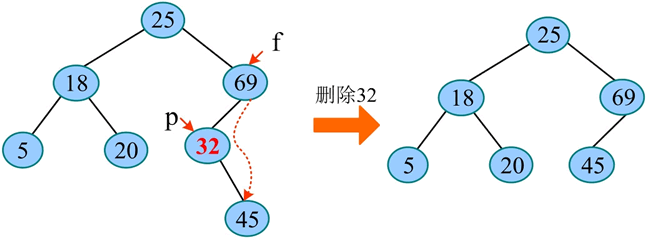
1) 左子树为空。如下图所示,在二叉搜索树中删除 32,首先找到 32 所在的位置,若其左子树为空,则令其右子树“子承父业”代替其位置。
2) 右子树为空。如下图所示,在二叉搜索树中删除 69,首先找到 69 所在的位置,若其右子树为空,则令其左子树“子承父业”代替其位置。
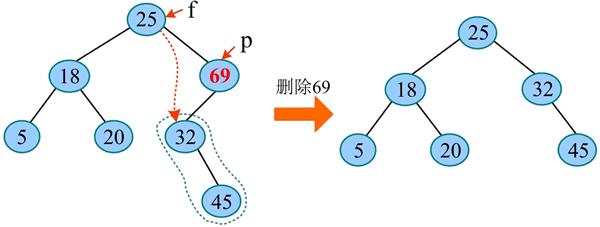
3) 左、右子树均不为空。如下图所示,在二叉搜索树中删除 25,首先找到 25 所在的位置,判断其左、右子树均不为空,首先令其直接前驱(左子树最右节点 20)代替它,再删除其直接前驱 20 即可。删除 20 时,其左子树“子承父业”代替其位置。
二叉搜索树删除元素的算法实现:
顺序查找和二分查找都适用于静态查找,若在查找过程中有插入、删除等修改操作,则在最坏情况和平均情况下的时间复杂度都为 O(n)。
是否存在一种数据结构和算法,既可以高效地查找,又可以高效地动态修改?实际上,将二分查找与二叉树结合起来,可以实现二叉搜索树结构,达到单次修改和查找的时间复杂度均为 O(logn)。
二叉搜索树(Binary Search Tree,BST),又叫作“二叉查找树”“二叉排序树”,是一种对查找和排序都有用的特殊的二叉树。
二叉搜索树或是空树,或是满足如下性质的二叉树:
- 若其左子树不为空(即为非空树),则左子树上所有节点的值均小于根的值;
- 若其右子树不为空,则右子树上所有节点的值均大于根的值;
- 其左、右子树本身又是一棵二叉搜索树。
二叉搜索树的特性:左子树<根<右子树。二叉搜索树的中序遍历序列是一个递增序列。例如,一棵二叉搜索树,其中序遍历序列如下图所示。

二叉搜索树查找目标元素
二叉搜索树的中序遍历序列具有有序性,所以其在查找方面与二分查找类似,即每次都缩小查找范围,查找效率较高。算法步骤:
- 若二叉搜索树为空(即为空树),查找失败,则返回空指针。
-
若二叉搜索树不为空,则将待查找关键字 x 与根的关键字 T->data 进行比较:
- 若 x=T->data,查找成功,则返回 T;
- 若 x<T->data,则递归查找左子树;
- 若 x>T->data,则递归查找右子树。
例如,一棵二叉搜索树如下图所示,查找关键字 32:

1) 将 32 与二叉搜索树的根 25 进行比较,32>25,在右子树中查找:

2) 将 32 与右子树的根 69 进行比较,32<69,在左子树中查找:

3) 将 32 与左子树的根 32 进行比较,相等,查找成功:

二叉搜索树查找算法实现:
BSTree SearchBST(BSTree T, int key) { //在二叉搜索树中进行查找操作
//若查找成功,则返回指向该节点的指针,否则返回空指针
if((!T) || key == T->data)
return T;
else if(key < T->data)
return SearchBST(T->lchild, key); //在左子树中查找
else
return SearchBST(T->rchild, key); //在右子树中查找
}
在二叉搜索树中进行查找操作的时间复杂度与树的形态有关,可分为最好情况、最坏情况和平均情况进行分析:1) 在最好情况下,二叉搜索树与二分查找的判定树形态相似,如下图所示。每次查找范围都可以缩小一半,查找路径最多从根到叶子,比较次数最多为树的高度 logn,在最好情况下进行查找操作的时间复杂度为 O(logn)。

2) 在最坏情况下,二叉搜索树为单支树,只有左子树或右子树,如下图所示。每次查找范围都缩小为 n-1 个元素,退化为顺序查找,在最坏情况下进行查找操作的时间复杂度为 O(n)。

3) 在平均情况下,有 n 个节点的二叉搜索树有 Cn 棵(Cn 为卡特兰数),可以证明,在平均情况下进行查找操作的时间复杂度也为 O(logn)。
二叉搜索树插入目标元素
首先在二叉搜索树中查找待插入关键字,当查找不成功时,再将待插入关键字作为新叶子插入查找的最后一个节点的左孩子或右孩子位置。在二叉搜索树中不允许有重复的节点,若查找成功,则什么也不做,或者增加一个数量域,记录该关键字的出现次数。算法步骤:
- 若二叉搜索树为空,则创建一个新节点 s,将待插入关键字放入新节点的数据域,将 s 作为根,左、右子树均为空;
-
若二叉搜索树不为空,则将待查找关键字 x 与根的关键字 T->data 进行比较:
- 若 x<T->data,则将 x 插入左子树。
- 若 x>T->data,则将 x 插入右子树。
例如,一棵二叉搜索树如下图所示,向其中插入关键字 30。

1) 将 30 与根 25 进行比较,30>25,在 25 的右子树中查找:

2) 将 30 与右子树的根 69 进行比较,30<69,在 69 的左子树中查找:

3) 将 30 与左子树的根 32 进行比较,30<32,在 32 的左子树中查找:

4) 32 的左子树为空,将 30 作为新叶子插入 32 的左子树:

二叉搜索树插入算法实现:
void InsertBST(BSTree &T, int x) { //在二叉搜索树中进行插入操作
if (!T) { //若为空树
BSTree s = new BSTNode; //生成新节点 s
s->data = x; //s 的数据域为 x
s->lchild = s->rchild = NULL; //将 s 作为叶子
T = s; //将 s 链接到已找到的插入位置
return;
}
if (x == T->data) return; //若查找成功,则什么也不做
if (x < T->data)
InsertBST(T->lchild, x); //插入左子树
else if (x > T->data)
InsertBST(T->rchild, x); //插入右子树
}
在二叉搜索树中进行插入操作时,需要先查找插入位置,插入本身只需常数时间,但查找插入位置的时间复杂度为 O(logn)。二叉搜索树创建元素
下面从空树开始依次输入关键字并进行创建操作,最终得到一棵二叉搜索树。算法实现:
void CreateBST(BSTree &T) { //在二叉搜索树中进行创建操作
T = NULL;
int x;
cin >> x;
while (x != ENDFLAG) { //ENDFLAG 为自定义常量,作为输入结束标志
InsertBST(T, x); //插入二叉搜索树 T
cin >> x;
}
}
每次进行插入操作,在最好情况和平均情况下的时间复杂度为 O(logn),在最坏情况下的时间复杂度为 O(n)。二叉搜索树的创建需要 n 次插入,在最好情况和平均情况下的时间复杂度为 O(nlogn),在最坏情况下的时间复杂度为 O(n^2),相当于把一个无序序列转换为一个有序序列的排序过程。实质上,创建二叉搜索树与快速排序一样,根相当于快速排序中的基准元素,左、右部分的划分情况取决于基准元素。输入序列的次序不同,创建的二叉搜索树也不同。
二叉搜索树删除元素
首先在二叉搜索树中找到待删除节点,然后执行删除操作。假设指针 p 指向待删除节点,指针 f 指向 p 的双亲。根据待删除节点所在位置的不同,具体的删除操作也不同,可分为下面三种情况。
1) 被删除节点的左子树为空。若被删除节点的左子树为空,则令其右子树“子承父业”代替其位置即可。例如,在二叉搜索树中删除 P,如下图所示。

2) 被删除节点的右子树为空。若被删除节点的右子树为空,则令其左子树“子承父业”代替其位置即可,如下图所示。

3) 被删除节点的左、右子树均不为空。若被删除节点的左子树和右子树均不为空,则无法再“子承父业”了。
根据二叉搜索树的中序遍历有序性,删除该节点时,可以首先用其直接前驱(或直接后继)代替其位置,然后删除其直接前驱(或直接后继)即可。
那么,在中序遍历序列中,一个节点的直接前驱(或直接后继)是哪个节点呢?
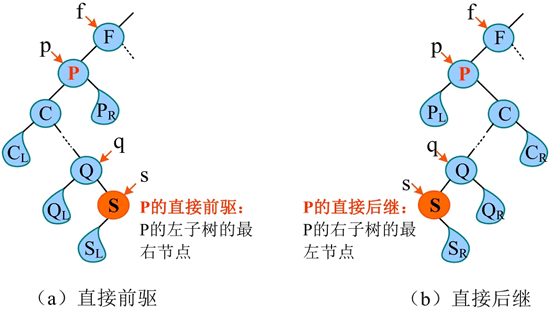
- 直接前驱:在中序遍历序列中,如下图(a)所示,P 的直接前驱为其左子树的最右节点,则沿着 P 的左子树一直访问其右子树,直到没有右子树,就找到了最右节点。
- 直接后继:在中序遍历序列中,如下图(b)所示,P 的直接后继为其右子树的最左节点。s 指向 p 的直接后继,q 指向 s 的双亲。f、p、q、s 为指向节点的指针,也可以代指该节点。

以 P 的直接前驱 S 代替 P,之后删除 S 即可。S 为最右节点,没有右子树,删除 S 后,左子树“子承父业”代替 S,如下图所示。

例如,在二叉搜索树中删除 24。首先找到 24 的位置 p,然后找到 p 的直接前驱 22,把 22 代替 24,删除 22,删除过程如下图所示。

删除节点之后是不是仍然满足二叉搜索树的中序遍历有序性?
需要注意的是,有一种特殊情况:如下图所示,P 的左孩子没有右子树,S 就是其左子树的最右节点(直接前驱),则首先用 S 代替 P,然后删除 S 即可。S 为最右节点且没有右子树,删除 S 后,左子树“子承父业”代替 S。

例如,在二叉搜索树中删除 20,删除过程如下图所示。

二叉搜索树删除元素的算法步骤如下:
- 在二叉搜索树中查找待删除关键字,p 指向待删除节点,f 指向 p 的双亲,若查找失败,则返回。
-
若查找成功,则分下面三种情况进行删除操作:
- 若被删除节点的左子树为空,则令其右子树“子承父业”代替其位置。
- 若被删除节点的右子树为空,则令其左子树“子承父业”代替其位置。
- 若被删除节点的左、右子树均不为空,则首先令其直接前驱(或直接后继)代替它,再删除其直接前驱(或直接后继)。
1) 左子树为空。如下图所示,在二叉搜索树中删除 32,首先找到 32 所在的位置,若其左子树为空,则令其右子树“子承父业”代替其位置。

2) 右子树为空。如下图所示,在二叉搜索树中删除 69,首先找到 69 所在的位置,若其右子树为空,则令其左子树“子承父业”代替其位置。

3) 左、右子树均不为空。如下图所示,在二叉搜索树中删除 25,首先找到 25 所在的位置,判断其左、右子树均不为空,首先令其直接前驱(左子树最右节点 20)代替它,再删除其直接前驱 20 即可。删除 20 时,其左子树“子承父业”代替其位置。

二叉搜索树删除元素的算法实现:
void DeleteBST(BSTree &T, int x) { //在二叉搜索树中进行删除操作
BSTree p = T, f = NULL, q, s;
if (!T) return; //树为空则返回
while (p) { //查找
if (x == p->data) break; //找到关键字等于 x 的节点 p,结束循环
f = p; //f 为 p 的双亲
if (x < p->data)
p = p->lchild; //在 p 的左子树中继续查找
else
p = p->rchild; //在 p 的右子树中继续查找
}
if (!p) return; //找不到被删除节点则返回
//三种情况:p 的左、右子树均不为空、无右子树、无左子树
if ((p->lchild) && (p->rchild)) { //被删除节点 p 的左、右子树均不为空
q = p;
s = p->lchild;
while (s->rchild) { //查找其前驱,即 p 的左子树的最右节点
q = s;
s = s->rchild;
}
p->data = s->data; //将 s 的值赋值给被删除节点 p,然后删除 s
if (q != p)
q->rchild = s->lchild; //重接 q 的右子树
else
q->lchild = s->lchild; //重接 q 的左子树
delete s;
}
else {
if (!p->rchild) { //被删除节点 p 无右子树,只需重接其左子树
q = p;
p = p->lchild;
}
else if (!p->lchild) { //被删除节点 p 无左子树,只需重接其右子树
q = p;
p = p->rchild;
}
/* ——将 p 所指的子树挂接到其双亲 f 相应的位置—— */
if (!f)
T = p; //被删除节点为根
else if (q == f->lchild)
f->lchild = p; //挂接到 f 的左子树位置
else
f->rchild = p; //挂接到 f 的右子树位置
delete q;
}
}
在二叉搜索树中进行删除操作时主要进行的是查找操作,时间复杂度为 O(logn)。在删除过程中,若需要查找被删除节点的直接前驱,则时间复杂度为 O(logn)。所以,在二叉搜索树中进行删除操作的时间复杂度为 O(logn)。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: