二叉排序树详解(Java实现)
二叉排序树也称为二叉查找树,二叉排序树的查找是一种常用的动态查找方法。
动态查找是指在查找的过程中动态生成表结构,对于给定的关键字,若表中存在该关键字,则返回其位置,表示查找成功,否则插入该关键字的元素。
下面介绍二叉排序树的查找、插入和删除。
显然,这是一个递归的定义。下图所示为一棵二叉排序树。图中的每个结点是对应元素关键字的值。
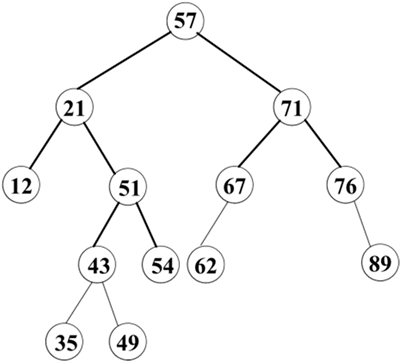
图 1 二叉排序树
从图 1 可以看出,图中的每个结点的值都大于其所有左子树结点的值,而小于其所有右子树结点的值。若要查找与二叉树中某个关键字相等的结点,则可以从根结点开始,与给定的关键字比较:
采用二叉树的链式存储结构,二叉排序树的类型定义如下:
二叉排序树的查找算法描述如下:
利用二叉排序树的查找算法的思想,若要查找关键字为 x.key=62 的元素,则从根结点开始,依次将该关键字与二叉树的根结点比较:
如果要查找关键字为 23 的元素,当比较到结点为 12 的元素时,因为关键字 12 对应的结点不存在右子树,所以查找失败,返回 null。
在二叉排序树的查找过程中,查找某个结点的过程正好是走了从根结点到要查找的结点的路径,其比较的次数正好是路径长度 +1,这类似于折半查找,区别在于,由 n 个结点构成的判定树是唯一的,而由 n 个结点构成的二叉排序树则不唯一(与结点的顺序有关)。
例如,如下图所示为两棵二叉排序树,其元素的关键字序列分别是 {57,21,71,12,51,67,76} 和 {12,21,51,57,67,71,76}。
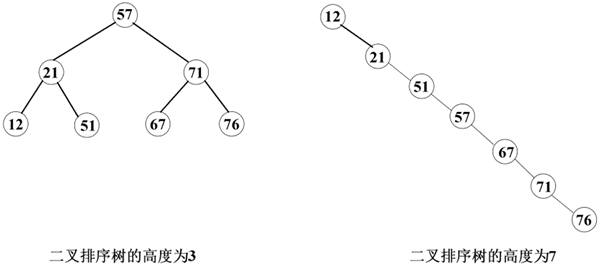
图 2 两种不同形态的二叉排序树
在图 2 中,假设每个元素的查找概率都相等,则左边的树的平均查找长度为:
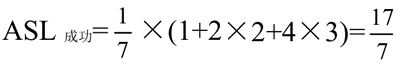
右边的树的平均查找长度为:
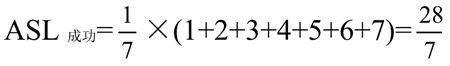
因此,树的平均查找长度与树的形态有关。若二叉排序树有 n 个结点,则在最坏的情况下,平均查找长度为 (n+1)/2。在最好的情况下,平均查找长度为 logn。
二叉树的插入操作从根结点开始,首先要检查当前结点是不是要查找的元素,若是,则不进行插入操作,否则将结点插入查找失败时结点的左指针或右指针处。
在算法的实现过程中,需要设置一个指向下一个要访问结点的双亲结点指针 parent,就是需要记下前驱结点的位置,以便在查找失败时进行插入操作。
假设当前结点指针 cur 为空,则说明查找失败,需要插入结点:
若二叉排序树为空树,则使当前结点成为根结点。在整个二叉排序树的插入过程中,其插入操作都是在叶子结点处进行的。
二叉排序树的插入操作算法描述如下:
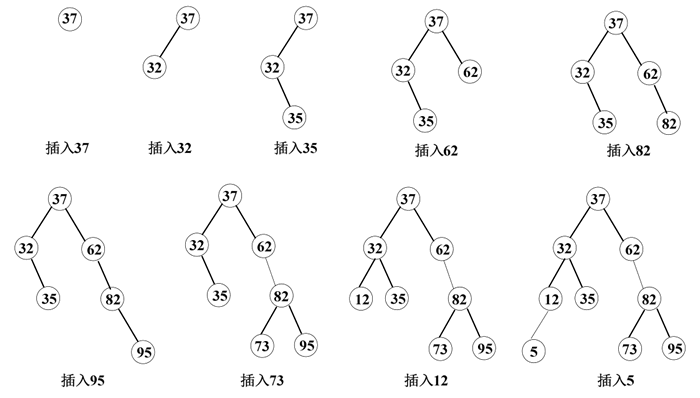
图 5 二叉排序树的插入过程
从图 5 中可以看出,通过中序遍历二叉排序树,可以得到一个关键字有序的序列 {5,12,32,35,37,62,73,82,95}。
因此,构造二叉排序树的过程就是对一个无序的序列排序的过程,且每次插入的结点都是叶子结点,在二叉排序树的插入过程中,不需要移动结点,仅需要移动结点指针,实现起来较为容易。
假设要删除的结点为 S,由 S 指示,p 指向 S 的双亲结点,设 S 为 p 的左孩子结点。二叉排序树的各种删除情形如下图所示。
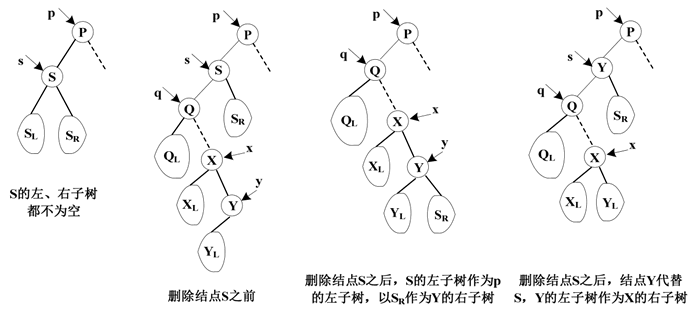
图 6 二叉排序树的删除操作的各种情形
1) 如果 S 指向的结点为叶子结点,其左子树和右子树为空,删除叶子结点不会影响树的结构特性,因此只需要修改 p 的指向即可。
2) 如果 S 指向的结点只有左子树或右子树,在删除结点 S 后,只需要将 S 的左子树 SL 或右子树 SR 作为 p 的左孩子,即 p.lchild=s.lchild 或 p.lchid=s.rchild。
3) 如果 S 的左子树和右子树都存在,在删除结点 S 之前,二叉排序树的中序序列为 {…QLQ…XLXYLYSSRP…},因此,在删除结点 S 之后,有两种方法调整使该二叉树仍然保持原来的性质不变:
通过这两种方法均可以使二叉排序树的性质不变。
二叉排序树的删除操作算法描述如下:
分析:通过给定一组元素值,利用插入算法将元素插入二叉树中构成一棵二叉排序树,然后利用查找算法实现二叉排序树的查找。
动态查找是指在查找的过程中动态生成表结构,对于给定的关键字,若表中存在该关键字,则返回其位置,表示查找成功,否则插入该关键字的元素。
下面介绍二叉排序树的查找、插入和删除。
二叉排序树的定义与查找
所谓二叉排序树,要么是一棵空二叉树,要么二叉树具有以下性质:- 若二叉树的左子树不为空,则左子树上的每一个结点的值都小于其对应根结点的值。
- 若二叉树的右子树不为空,则右子树上的每一个结点的值都大于其对应根结点的值。
- 该二叉树的左子树和右子树满足性质 1 和性质 2,即左子树和右子树也是一棵二叉排序树。
显然,这是一个递归的定义。下图所示为一棵二叉排序树。图中的每个结点是对应元素关键字的值。

图 1 二叉排序树
从图 1 可以看出,图中的每个结点的值都大于其所有左子树结点的值,而小于其所有右子树结点的值。若要查找与二叉树中某个关键字相等的结点,则可以从根结点开始,与给定的关键字比较:
- 若相等,则查找成功;
- 若给定的关键字小于根结点的值,则在该根结点的左子树中查找;
- 若给定的关键字大于根结点的值,则在该根结点的右子树中查找。
采用二叉树的链式存储结构,二叉排序树的类型定义如下:
class BTNode {
int data;
BTNode lchild, rchild;
BTNode(int data, BTNode lchild, BTNode rchild) {
this.data = data;
this.lchild = lchild;
this.rchild = rchild;
}
BTNode(int data) {
this.data = data;
this.lchild = this.rchild = null;
}
BTNode() {
}
}
二叉排序树的查找算法描述如下:
public class BiSearchTree {
BTNode root;
BiSearchTree() {
root = null;
}
public void CreateBiSearchTree(int table[]) {
for (int i = 0; i < table.length; i++)
BSTInsert2(table[i]);
}
public BTNode BSTSearch(int x) {
// 二叉排序树的查找,若找到元素 x,则返回指向结点的指针,否则返回 null
BTNode p = root;
if (root != null) {
p = root;
while (p != null) {
if (p.data == x) // 若找到,则返回指向该结点的指针
return p;
else if (x < p.data) // 若关键字小于 p 指向的结点的值,则在左子树中查找
p = p.lchild;
else
p = p.rchild; // 若关键字大于 p 指向的结点的值,则在右子树中查找
}
}
return null;
}
}
利用二叉排序树的查找算法的思想,若要查找关键字为 x.key=62 的元素,则从根结点开始,依次将该关键字与二叉树的根结点比较:
- 因为有 62>57,所以需要在结点为 57 的右子树中进行查找;
- 因为有 62<71,所以需要在以 71 为结点的左子树中继续查找;
- 因为有 62<67,所以需要在结点为 67 的左子树中查找;
- 因为该关键字与结点为 67 的左孩子结点对应的关键字相等,所以查找成功,返回结点 62 对应的指针。
如果要查找关键字为 23 的元素,当比较到结点为 12 的元素时,因为关键字 12 对应的结点不存在右子树,所以查找失败,返回 null。
在二叉排序树的查找过程中,查找某个结点的过程正好是走了从根结点到要查找的结点的路径,其比较的次数正好是路径长度 +1,这类似于折半查找,区别在于,由 n 个结点构成的判定树是唯一的,而由 n 个结点构成的二叉排序树则不唯一(与结点的顺序有关)。
例如,如下图所示为两棵二叉排序树,其元素的关键字序列分别是 {57,21,71,12,51,67,76} 和 {12,21,51,57,67,71,76}。

图 2 两种不同形态的二叉排序树
在图 2 中,假设每个元素的查找概率都相等,则左边的树的平均查找长度为:
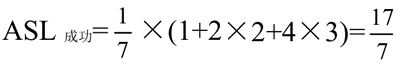
右边的树的平均查找长度为:
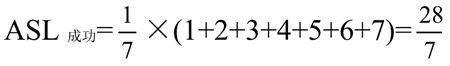
因此,树的平均查找长度与树的形态有关。若二叉排序树有 n 个结点,则在最坏的情况下,平均查找长度为 (n+1)/2。在最好的情况下,平均查找长度为 logn。
二叉排序树的插入操作
二叉排序树的插入操作过程其实就是二叉排序树的建立过程。二叉树的插入操作从根结点开始,首先要检查当前结点是不是要查找的元素,若是,则不进行插入操作,否则将结点插入查找失败时结点的左指针或右指针处。
在算法的实现过程中,需要设置一个指向下一个要访问结点的双亲结点指针 parent,就是需要记下前驱结点的位置,以便在查找失败时进行插入操作。
假设当前结点指针 cur 为空,则说明查找失败,需要插入结点:
- 若 parent.data 小于要插入的结点 x,则需要将 parent 的左指针指向 x,使 x 成为 parent 的左孩子结点;
- 若 parent.data 大于要插入的结点 x,则需要将 parent 的右指针指向 x,使 x 成为 parent 的右孩子结点;
若二叉排序树为空树,则使当前结点成为根结点。在整个二叉排序树的插入过程中,其插入操作都是在叶子结点处进行的。
二叉排序树的插入操作算法描述如下:
public void BSTInsert(int x)
// 二叉排序树的插入操作,若树中不存在元素 x,则将 x 插入正确的位置
{
if (root == null) {
root = new BTNode(x);
return;
}
BTNode parent = root;
while (true) {
int e = parent.data;
if (x < e) {
if (parent.lchild == null)
parent.lchild = new BTNode(x);
else
parent = parent.lchild;
} else if (x > e) {
if (parent.rchild == null)
parent.rchild = new BTNode(x);
else
parent = parent.rchild;
} else
return;
}
}
}
对于一个关键字序列 {37,32,35,62,82,95,73,12,5},根据二叉排序树的插入算法的思想,对应的二叉排序树的插入过程如下图所示:
图 5 二叉排序树的插入过程
从图 5 中可以看出,通过中序遍历二叉排序树,可以得到一个关键字有序的序列 {5,12,32,35,37,62,73,82,95}。
因此,构造二叉排序树的过程就是对一个无序的序列排序的过程,且每次插入的结点都是叶子结点,在二叉排序树的插入过程中,不需要移动结点,仅需要移动结点指针,实现起来较为容易。
注意,即使结点相同,插入的结点顺序不同,其二叉排序树的形态也不一样。
二叉排序树的删除操作
在二叉排序树中删除一个结点后,剩下的结点仍然构成一棵二叉排序树,即保持原来的特性。删除二叉排序树中的一个结点可以分为 3 种情况讨论。假设要删除的结点为 S,由 S 指示,p 指向 S 的双亲结点,设 S 为 p 的左孩子结点。二叉排序树的各种删除情形如下图所示。

图 6 二叉排序树的删除操作的各种情形
1) 如果 S 指向的结点为叶子结点,其左子树和右子树为空,删除叶子结点不会影响树的结构特性,因此只需要修改 p 的指向即可。
2) 如果 S 指向的结点只有左子树或右子树,在删除结点 S 后,只需要将 S 的左子树 SL 或右子树 SR 作为 p 的左孩子,即 p.lchild=s.lchild 或 p.lchid=s.rchild。
3) 如果 S 的左子树和右子树都存在,在删除结点 S 之前,二叉排序树的中序序列为 {…QLQ…XLXYLYSSRP…},因此,在删除结点 S 之后,有两种方法调整使该二叉树仍然保持原来的性质不变:
- 第一种方法是使结点 S 的左子树作为结点 P 的左子树,结点 S 的右子树成为结点 Y 的右子树;
- 第二种方法是使结点 S 的直接前驱取代结点 S,并删除 S 的直接前驱结点 Y,然后令结点 Y 原来的左子树作为结点 X 的右子树。
通过这两种方法均可以使二叉排序树的性质不变。
二叉排序树的删除操作算法描述如下:
public boolean BSTDelete(int x)
// 在二叉排序树 T 中存在值为 x 的数据元素时,删除该数据元素结点,并返回 true,否则返回 false
{
BTNode p = null;
if (s == null) // 若不存在值为 x 的数据元素,则返回 false
{
System.out.println("二叉树为空,不能进行删除操作");
return false;
}
else {
while (s != null) {
if (s.data != x)
p = s; // 若找到值为 x 的数据元素,则 s 为要删除的结点
else
break;
if (x < s.data) // 若当前元素的值大于 x 的值,则在该结点的左子树中查找并删除
s = s.lchild;
else
s = s.rchild; // 若当前元素的值小于 x 的值,则在该结点的右子树中查找并删除
}
}
// 从二叉排序树中删除结点 s,并使该二叉排序树的性质不变
if (s.lchild == null) // 若 s 的左子树为空,则使 s 的右子树成为被删除结点的双亲结点的左子树
{
if (p == null)
root = s.rchild;
else if (s == p.lchild)
p.lchild = s.rchild;
else
p.rchild = s.rchild;
return true;
}
if (s.rchild == null) // 若 s 的右子树为空,则使 s 的左子树成为被删除结点的双亲结点的左子树
{
if (p == null)
root = s.lchild;
else if (s == p.lchild)
p.lchild = s.lchild;
else
p.rchild = s.lchild;
return true;
}
// 若 s 的左、右子树都存在,则使 s 的左驱前驱结点代替 s,并使其直接前驱结点的左子树成为其双亲结点的右子树结点
BTNode x_node = s;
BTNode y_node = s.lchild;
while (y_node.rchild != null) {
x_node = y_node;
y_node = y_node.rchild;
}
s.data = y_node.data; // 结点 s 被 y_node 取代
if (x_node != s) // 如果结点 s 的左孩子结点存在右子树
x_node.rchild = y_node.lchild; // 使 y_node 的左子树成为 x_node 的右子树
else // 如果结点 s 的左孩子结点不存在右子树
x_node.lchild = y_node.lchild; // 使 y_node 的左子树成为 x_node 的左子树
return true;
}
删除二叉排序树中的任意一个结点后,二叉排序树的性质保持不变。二叉排序树的应用举例
给定一组元素序列 {37, 32, 35, 62, 82, 95, 73, 12, 5},利用二叉排序树的插入算法创建一棵二叉排序树,然后查找元素值为32的元素,并删除该元素,然后以中序序列输出该元素序列。分析:通过给定一组元素值,利用插入算法将元素插入二叉树中构成一棵二叉排序树,然后利用查找算法实现二叉排序树的查找。
public static void main(String args[]) {
int table[] = {37, 32, 35, 62, 82, 95, 73, 12, 5};
BiSearchTree S = new BiSearchTree();
S.CreateBiSearchTree(table);
BTNode T = S.root;
System.out.println("中序遍历二叉排序树得到的序列为: ");
S.InOrderTraverse(T);
Scanner sc = new Scanner(System.in);
System.out.println("\n请输入要查找的元素: ");
int x = Integer.parseInt(sc.nextLine());
BTNode p = S.BSTSearch(x);
if (p != null)
System.out.println("二叉排序树查找,关键字" + x + "存在!");
else
System.out.println("查找失败!");
S.BSTDelete(x);
System.out.println("删除" + x + "后,二叉排序树的元素序列: ");
S.InOrderTraverse(T);
}
程序运行结果如下:
中序遍历二叉排序树得到的序列为: 5 12 32 35 37 62 73 82 95 请输入要查找的元素:62 二叉排序树查找,关键字62存在! 删除62后,二叉排序树的元素序列: 5 12 32 35 37 73 82 95
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: