并查集(超级详细,动图演示)
数据结构里汇集了很多种存储结构,包括线性表、树、图等,它们还可以进行更细致地划分,每一种结构都有其特定的用途和优势。
拿最简单的线性表举例,它专门存储逻辑关系是“一对一”的数据。线性表又可以细分为顺序表和链表,顺序表擅长对目标元素的查询操作,而链表擅长对目标元素的添加(插入)和删除操作。
本节给大家讲解的并查集,也是一种存储结构,它可以存储多个集合,特别擅长处理集合的合并(Union)和查询(Find)操作。
这里提到的集合,与数学里的集合非常类似,可以存放一组元素,它的特点是:
例如,{1, 2, 3} 是一个集合,它和
集合的合并操作,指的是将两个独立的集合整合成一个大的集合,比如将 {1, 2} 和 {3} 合并为 {1, 2, 3};集合的查询操作,指的是查找目标元素属于哪个集合。
搞清楚并查集是什么之后,接下来讲解并查集的具体实现。
给定一个并查集,我们可以把它里面的每个集合想象成一棵树结构(注意不是二叉树,是多叉树),那么整个并查集就是一个森林。假设
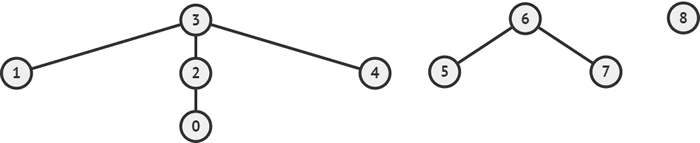
图 1 想象成森林的并查集
在图 1 的基础上,可以很轻松地完成集合的合并和查询操作:
1) 合并两个集合,只需要找到它们各自的树根结点,再把两个树根结点相连即可,如下图所示:
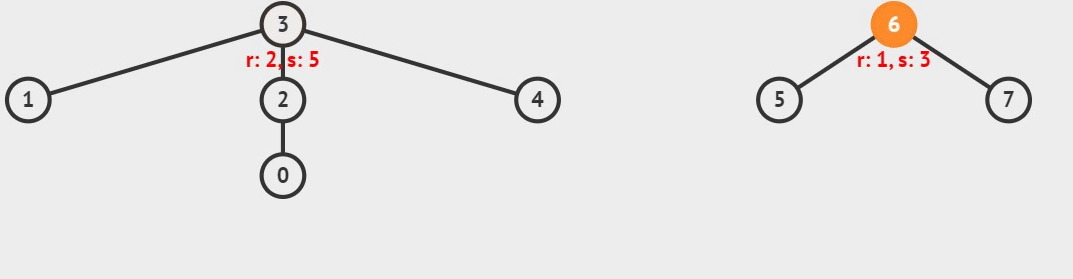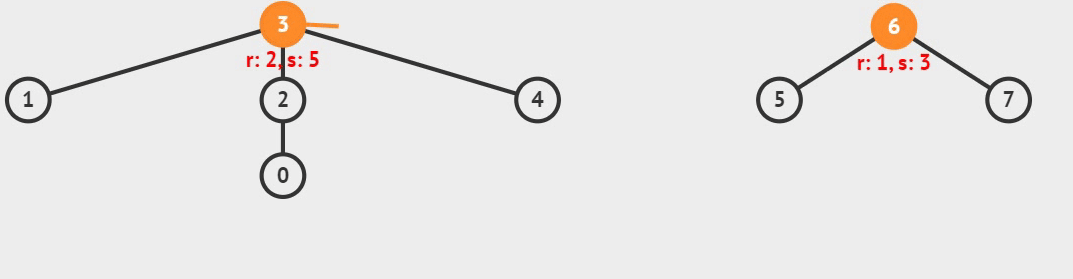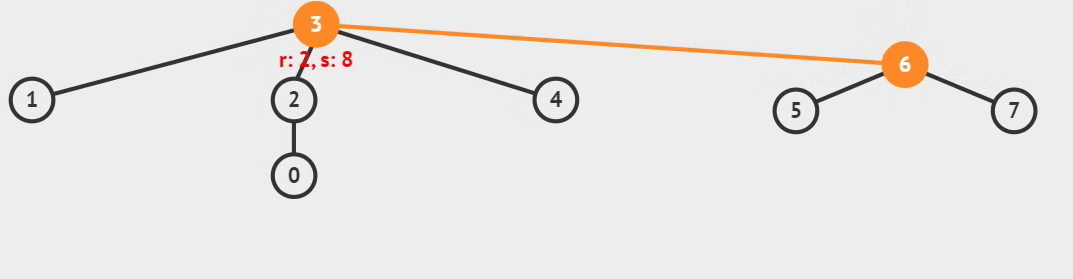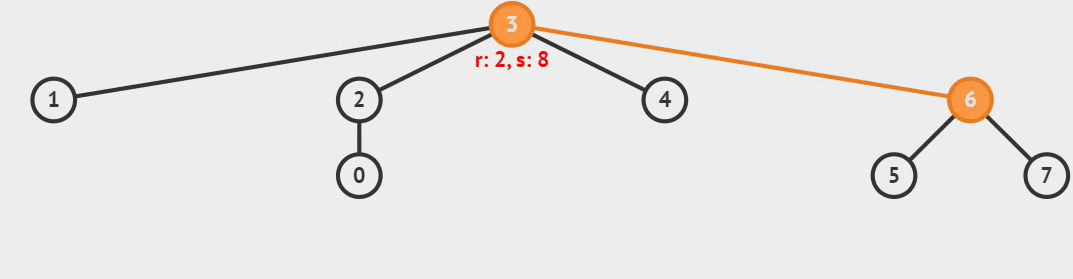
图 2 集合的合并操作
2) 查询某个元素位于哪个集合,等同于确定该元素位于哪棵树上。我们习惯选择树根结点代表整棵树(把位于树根的元素作为整个集合的代表),因为只要树的根结点存在,整棵树就一直存在。
仔细观察图 2,两棵树未整合之前,元素 5 位于根结点是 6 的树上(5 位于代表元素是 6 的集合里);两棵树整合之后,元素 5 所在的树成为了另一棵树的一部分,元素 5 就位于根结点是 3 的树上(5 位于代表元素是 3 的集合里)。
在上述的讲解中,我们把并查集想象成是森林,把并查集里的集合想象成一棵棵的树,实现了集合的合并和查询操作。然而真正落地、写代码实现并查集,用的不是复杂的树形结构,而是顺序表(一维数组)。
假设并查集内有 3 个集合,分别是{0, 1, 2, 3, 4}、{5, 6, 7} 和 {8}。想要将这 3 个集合存放到数组里,除了存储所有元素的值之外,还要存储各个元素之间的关系,存储方案是:
存储
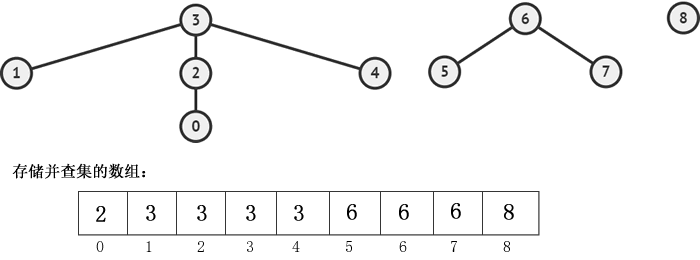
仔细观察图 3 下方的数组:
0 和 2、2 和 3、1 和 3、4 和 3 都位于同一个集合,表明 {0, 1, 2, 3, 4} 是并查集中的一个集合,并且这个集合的代表元素是 3。同样的道理,可以得出 {5, 6, 7} 是一个集合,代表元素是 6;{8} 是一个集合,代表元素是 8。
你看,一维数组既存储了并查集中的全部元素,又存储了元素之间的关系,确实成功地存储了一个并查集。并查集可以用如下的 C 语言结构体表示:
那么,如何在一维数组中实现集合的合并和查询操作呢?
仔细观察图 2,合并两个集合的过程,其实只做了一件事,就是把两个集合的代表元素(树根结点)连接起来。因此,合并数组中的两个集合,只需要做两件事:
下面是实现合并两个集合的 C 语言代码:
我们知道,代表元素有一个很明显的特征,就是数组里存放的是它自己的位置下标。所以从目标元素开始,不断地查找当前元素的父结点,最终就能找到存储自己位置下标的元素,这个元素就是代表元素。
下面是 find() 函数的具体实现:
下面是实现并查集的完整 C 语言代码:
假设将并查集中的集合
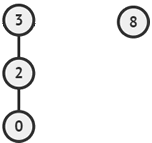
图 4 两个集合对应的树结构
调用上面程序中的 unionSets() 函数,合并后的树根结点可以是 3,也可以是 8,如下图所示:
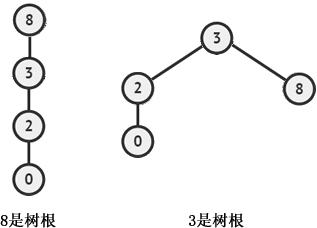
图 5 合并后集合对应的树
虽然两种方式都成功地合并了两个集合,但新集合的查询效率是不一样的。比如在两棵树中查找元素 0 的代表元素,查找的过程分别是:
显然合并后的树越高,集合的查询效率越低。这就意味着,要想并查集的查询效率尽可能高,要尽可能地降低各个集合对应的树的高度,下面介绍两种常用的实现方法。
注意,这种方法之所以称作“按秩合并”,而不是“按高合并”,因为方法中使用的树的高度是一个估值,而不是精准计算出来的,树高度的估值称为秩。
按秩合并的具体思路是:单独用一个数组记录各个集合对应的树的秩。初始状态下各个集合只有一个元素,它们的秩全部为 1。合并两个集合时,先比较代表元素的秩,然后选择秩大一方的树根结点作为新的树根结点。
下面是采用按秩合并的方式实现的并查集:
按秩合并是一种优化并查集的技术,它可以让每个集合对应的树尽可能矮,从而提高并查集的查询效率。
路径压缩指的是在查找目标元素时,对于沿途找到的每个元素(包括目标元素),把它们存储的父亲结点直接改成树根结点,也就是代表元素。这样做的好处是,下次再查找该集合里的元素时,就能快速找到代表元素,并查集的查找效率就提升了。
如下图所示,左侧是集合 {0,2,3,8} 最初对应的树,假设查找元素 0 所在的集合,采用路径压缩的技术查找完成后,整棵树就变成了右侧的状态。
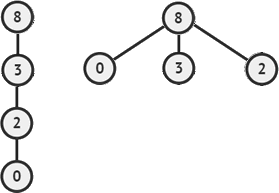
图 6 路径压缩优化技术
显然,经过路径压缩后的树变矮了,查找效率也就提升了。
路径压缩技术优化的是并查集的查询操作,也就是 C 语言程序中的 find() 函数,下面是引入路径压缩技术的 find() 函数:
按秩合并和路径压缩是两种常用的并查集优化技术,它们可以提升并查集的查询效率。
下面是实现并查集的 Java 程序:
下面是实现并查集的 Python 程序:
程序的运行结果为:
拿最简单的线性表举例,它专门存储逻辑关系是“一对一”的数据。线性表又可以细分为顺序表和链表,顺序表擅长对目标元素的查询操作,而链表擅长对目标元素的添加(插入)和删除操作。
本节给大家讲解的并查集,也是一种存储结构,它可以存储多个集合,特别擅长处理集合的合并(Union)和查询(Find)操作。
这里提到的集合,与数学里的集合非常类似,可以存放一组元素,它的特点是:
- 集合中的每个元素都是独一无二的,集合里不允许存在重复的元素;
- 集合中的元素是没有顺序的。
例如,{1, 2, 3} 是一个集合,它和
{3, 1, 2}是同一个集合,因为它们包含相同的元素。集合的合并操作,指的是将两个独立的集合整合成一个大的集合,比如将 {1, 2} 和 {3} 合并为 {1, 2, 3};集合的查询操作,指的是查找目标元素属于哪个集合。
搞清楚并查集是什么之后,接下来讲解并查集的具体实现。
并查集的实现
并查集可以存储多个集合,它能够高效地完成集合的合并和查询操作。给定一个并查集,我们可以把它里面的每个集合想象成一棵树结构(注意不是二叉树,是多叉树),那么整个并查集就是一个森林。假设
{0, 1, 2, 3, 4} {5, 6, 7} {8}是一个并查集,它是一个包含 3 棵树的森林,如下图所示:
图 1 想象成森林的并查集
在图 1 的基础上,可以很轻松地完成集合的合并和查询操作:
1) 合并两个集合,只需要找到它们各自的树根结点,再把两个树根结点相连即可,如下图所示:

图 2 集合的合并操作
像图 2 这样,通过连接两棵树的根结点,把两棵树整合成一棵树,就实现了把两个集合图中,r 指的是整棵树的高度(深度);s 指的是树中的结点数量。
{0, 1, 2, 3, 4} {5, 6, 7}合并成一个集合{0, 1, 2, 3, 4, 5, 6, 7}。2) 查询某个元素位于哪个集合,等同于确定该元素位于哪棵树上。我们习惯选择树根结点代表整棵树(把位于树根的元素作为整个集合的代表),因为只要树的根结点存在,整棵树就一直存在。
仔细观察图 2,两棵树未整合之前,元素 5 位于根结点是 6 的树上(5 位于代表元素是 6 的集合里);两棵树整合之后,元素 5 所在的树成为了另一棵树的一部分,元素 5 就位于根结点是 3 的树上(5 位于代表元素是 3 的集合里)。
在上述的讲解中,我们把并查集想象成是森林,把并查集里的集合想象成一棵棵的树,实现了集合的合并和查询操作。然而真正落地、写代码实现并查集,用的不是复杂的树形结构,而是顺序表(一维数组)。
假设并查集内有 3 个集合,分别是{0, 1, 2, 3, 4}、{5, 6, 7} 和 {8}。想要将这 3 个集合存放到数组里,除了存储所有元素的值之外,还要存储各个元素之间的关系,存储方案是:
- 将并查集里的每个元素各自对应一个数组下标。换句话说,用数组下标代表并查集里的元素;
- 把每个集合想象成一棵树,数组中负责记录各个元素的父亲结点的位置下标。树根结点比较特殊,它没有父亲结点,它对应的数组空间里存储的是自己的位置下标。
存储
{0, 1, 2, 3, 4} {5, 6, 7} {8}的并查集如下图所示:
图 3 存放多个集合的数组
仔细观察图 3 下方的数组:
- 下标 0 处存储的值是 2,表明元素 0 和 2 位于同一个集合里;
- 下标 1 存储的值是 3,表明 1 和 3 位于同一个集合;
- 下标 2 存储的值是 3,表明 2 和 3 位于同一个集合;
- 下标 3 存储的值是 3,它存储的是自己的下标值,表明它是一个树根结点,换句话说,它是一个集合的代表元素;
- 下标 4 存储的值是 3,表明 4 和 3 位于同一个集合。
0 和 2、2 和 3、1 和 3、4 和 3 都位于同一个集合,表明 {0, 1, 2, 3, 4} 是并查集中的一个集合,并且这个集合的代表元素是 3。同样的道理,可以得出 {5, 6, 7} 是一个集合,代表元素是 6;{8} 是一个集合,代表元素是 8。
你看,一维数组既存储了并查集中的全部元素,又存储了元素之间的关系,确实成功地存储了一个并查集。并查集可以用如下的 C 语言结构体表示:
typedef struct {
int parent[MAX_SIZE];
int count;
}UnionFind;
parent[] 数组用来存储并查集,count 用来统计并查集中的集合数量。那么,如何在一维数组中实现集合的合并和查询操作呢?
仔细观察图 2,合并两个集合的过程,其实只做了一件事,就是把两个集合的代表元素(树根结点)连接起来。因此,合并数组中的两个集合,只需要做两件事:
- 找到两个集合中的代表元素,假设是 x 和 y;
- 把 x 的父结点改成 y,或者把 y 的父结点改成 x,都可以实现 x 和 y 建立连接。
下面是实现合并两个集合的 C 语言代码:
// 合并两个元素所在的集合
void unionSets(UnionFind* uf, int x, int y) {
//找到两个元素所在集合的代表元素
int xRoot = find(uf, x);
int yRoot = find(uf, y);
//如果代表元素不同,表明它们是两个集合,将它们合并
if (xRoot != yRoot) {
uf->parent[xRoot] = yRoot; // uf->parent[yRoot] = xRoot;
}
}
程序中,find() 函数的功能是查询目标元素位于哪个集合,也就是找到它所在集合的代表元素。我们知道,代表元素有一个很明显的特征,就是数组里存放的是它自己的位置下标。所以从目标元素开始,不断地查找当前元素的父结点,最终就能找到存储自己位置下标的元素,这个元素就是代表元素。
下面是 find() 函数的具体实现:
// 查找根节点(代表元素)
int find(UnionFind* uf, int x) {
//如果数组中存储的值和它自身对应的数组下标相等,表明是集合的代表元素
if (uf->parent[x] == x) {
return x;
}
else {
return find(uf, uf->parent[x]);
}
}
这是一个递归函数,如果当前元素不是代表元素的话,函数会一直找到当前元素的父结点,直至找到代表元素。下面是实现并查集的完整 C 语言代码:
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 1000 // 可以根据需要调整最大尺寸
// 并查集数组
typedef struct {
int parent[MAX_SIZE];
int count;
}UnionFind;
// 初始化并查集
void initialize(UnionFind* uf, int size) {
for (int i = 0; i < size; i++) {
uf->parent[i] = i;
}
uf->count = size;
}
// 查找根节点(代表元素)
int find(UnionFind* uf, int x) {
//如果数组中存储的值和它自身对应的数组下标相等,表明是集合的代表元素
if (uf->parent[x] == x) {
return x;
}
else {
return find(uf, uf->parent[x]);
}
}
// 合并两个元素所在的集合
void unionSets(UnionFind* uf, int x, int y) {
//找到两个元素所在集合的代表元素
int xRoot = find(uf, x);
int yRoot = find(uf, y);
//如果代表元素不同,表明它们是两个集合,将它们合并
if (xRoot != yRoot) {
uf->parent[xRoot] = yRoot; // uf->parent[yRoot] = xRoot;
uf->count--;
}
}
// 主函数
int main() {
UnionFind uf;
initialize(&uf, 9);
unionSets(&uf, 0, 2);
unionSets(&uf, 2, 3);
unionSets(&uf, 1, 3);
unionSets(&uf, 4, 3);
unionSets(&uf, 5, 6);
unionSets(&uf, 7, 6);
printf("并查集中有 %d 个集合\n", uf.count);
if (find(&uf, 0) == find(&uf, 4)) {
printf("0和4在同一个集合里\n");
}
else
{
printf("0和4不在同一个集合里\n");
}
if (find(&uf, 8) == find(&uf, 5)) {
printf("8和5在同一个集合里\n");
}
else
{
printf("8和5不在同一个集合里\n");
}
return 0;
}
运行结果为:
并查集中有 3 个集合
0和4在同一个集合里
8和5不在同一个集合里
优化并查集的实现过程
为了方便理解,前面带领大家实现的是一个基础版(丐版)的并查集,并查集的查询效率还有提升的空间。假设将并查集中的集合
{1,2,3}与{8}合并,它们对应的树结构如下图所示:
图 4 两个集合对应的树结构
调用上面程序中的 unionSets() 函数,合并后的树根结点可以是 3,也可以是 8,如下图所示:

图 5 合并后集合对应的树
虽然两种方式都成功地合并了两个集合,但新集合的查询效率是不一样的。比如在两棵树中查找元素 0 的代表元素,查找的过程分别是:
- 8 作为树根:0 -> 2 -> 3 -> 8,查找过程要经过 2 和 3 两个结点;
- 3 作为树根:0 -> 2 -> 3,查找过程经过 2 这一个结点。
显然合并后的树越高,集合的查询效率越低。这就意味着,要想并查集的查询效率尽可能高,要尽可能地降低各个集合对应的树的高度,下面介绍两种常用的实现方法。
1) 按秩合并
所谓按秩合并,就是在合并两个集合的时候,先比较两棵树的高度,然后选择较高一方的根结点作为新树的根结点。注意,这种方法之所以称作“按秩合并”,而不是“按高合并”,因为方法中使用的树的高度是一个估值,而不是精准计算出来的,树高度的估值称为秩。
按秩合并的具体思路是:单独用一个数组记录各个集合对应的树的秩。初始状态下各个集合只有一个元素,它们的秩全部为 1。合并两个集合时,先比较代表元素的秩,然后选择秩大一方的树根结点作为新的树根结点。
下面是采用按秩合并的方式实现的并查集:
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 1000 // 可以根据需要调整最大尺寸
// 并查集数组
typedef struct {
int parent[MAX_SIZE];
int rank[MAX_SIZE];
int count;
}UnionFind;
// 初始化并查集
void initialize(UnionFind* uf, int size) {
for (int i = 0; i < size; i++) {
uf->parent[i] = i;
uf->rank[i] = 1;
}
uf->count = size;
}
// 查找根节点(代表元素)
int find(UnionFind* uf, int x) {
//如果数组中存储的值和它自身对应的数组下标相等,表明是集合的代表元素
if (uf->parent[x] == x) {
return x;
}
else {
return find(uf, uf->parent[x]);
}
}
// 合并两个元素所在的集合
void unionSets(UnionFind* uf, int x, int y) {
//找到两个元素所在集合的代表元素
int xRoot = find(uf, x);
int yRoot = find(uf, y);
//如果代表元素不同,表明它们是两个集合,将它们合并
if (xRoot != yRoot) {
// 按秩合并:将秩较小的树的根节点连接到秩较大的树上
if (uf->rank[xRoot] < uf->rank[yRoot]) {
uf->parent[xRoot] = yRoot;
} else if (uf->rank[xRoot] > uf->rank[yRoot]) {
uf->parent[yRoot] = xRoot;
} else { // 如果两棵树的秩相等,选择其中一棵作为根,并将其秩加1
uf->parent[yRoot] = xRoot;
uf->rank[xRoot] += 1;
}
uf->count--;
}
}
// 主函数
int main() {
UnionFind uf;
initialize(&uf, 9);
unionSets(&uf, 0, 2);
unionSets(&uf, 2, 3);
unionSets(&uf, 1, 3);
unionSets(&uf, 4, 3);
unionSets(&uf, 5, 6);
unionSets(&uf, 7, 6);
printf("并查集中有 %d 个集合\n", uf.count);
if (find(&uf, 0) == find(&uf, 4)) {
printf("0和4在同一个集合里\n");
}
else
{
printf("0和4不在同一个集合里\n");
}
if (find(&uf, 8) == find(&uf, 5)) {
printf("8和5在同一个集合里\n");
}
else
{
printf("8和5不在同一个集合里\n");
}
return 0;
}
和前面的基础版本相比,程序中做了两处改动:
- 在表示并查集的结构体中,添加了一个 rank[] 数组,用来记录各个集合对应的树的秩;
- 修改了 unionSets() 函数的实现过程。
按秩合并是一种优化并查集的技术,它可以让每个集合对应的树尽可能矮,从而提高并查集的查询效率。
4) 路径压缩
除了按秩合并,路径压缩也是并查集常用的优化技术。路径压缩指的是在查找目标元素时,对于沿途找到的每个元素(包括目标元素),把它们存储的父亲结点直接改成树根结点,也就是代表元素。这样做的好处是,下次再查找该集合里的元素时,就能快速找到代表元素,并查集的查找效率就提升了。
如下图所示,左侧是集合 {0,2,3,8} 最初对应的树,假设查找元素 0 所在的集合,采用路径压缩的技术查找完成后,整棵树就变成了右侧的状态。

图 6 路径压缩优化技术
显然,经过路径压缩后的树变矮了,查找效率也就提升了。
路径压缩技术优化的是并查集的查询操作,也就是 C 语言程序中的 find() 函数,下面是引入路径压缩技术的 find() 函数:
// 查找根节点(代表元素)
int find(UnionFind* uf, int x) {
if (uf->parent[x] != x) {
uf->parent[x] = find(uf, uf->parent[x]); // 路径压缩
}
return uf->parent[x];
}
和基础版本的 find() 相比,递归过程中增加了为 uf->parent[x] 赋值的过程,对于查找到的每个元素(包括目标元素),它们记录的父结点全部变成了代表元素。
总结
并查集是一种存储结构,擅长处理不同集合之间的合并和查询操作。并查集的应用场景有很多,特别是涉及图的连通性、元素分组之类的问题。按秩合并和路径压缩是两种常用的并查集优化技术,它们可以提升并查集的查询效率。
下面是实现并查集的 Java 程序:
public class UnionFind {
private int[] parent;
private int[] rank;
private int count;
// 构造函数,初始化并查集
public UnionFind(int size) {
parent = new int[size];
rank = new int[size];
count = size;
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
// 查找根节点(代表元素)
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]); // 路径压缩
}
return parent[x];
}
// 合并两个元素所在的集合
public void union(int x, int y) {
int xRoot = find(x);
int yRoot = find(y);
if (xRoot != yRoot) {
// 按秩合并
if (rank[xRoot] < rank[yRoot]) {
parent[xRoot] = yRoot;
} else if (rank[xRoot] > rank[yRoot]) {
parent[yRoot] = xRoot;
} else {
parent[yRoot] = xRoot;
rank[xRoot]++;
}
count--;
}
}
// 获取并查集中的集合数量
public int getCount() {
return count;
}
// 主函数,用于测试
public static void main(String[] args) {
UnionFind uf = new UnionFind(9);
uf.union(0, 2);
uf.union(2, 3);
uf.union(1, 3);
uf.union(4, 3);
uf.union(5, 6);
uf.union(7, 6);
System.out.println("并查集中有 " + uf.getCount() + " 个集合");
if (uf.find(0) == uf.find(4)) {
System.out.println("0和4在同一个集合里");
} else {
System.out.println("0和4不在同一个集合里");
}
if (uf.find(8) == uf.find(5)) {
System.out.println("8和5在同一个集合里");
} else {
System.out.println("8和5不在同一个集合里");
}
}
}
下面是实现并查集的 Python 程序:
class UnionFind:
def __init__(self, size):
self.parent = [i for i in range(size)]
self.rank = [1] * size
self.count = size
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x]) # 路径压缩
return self.parent[x]
def union(self, x, y):
x_root = self.find(x)
y_root = self.find(y)
if x_root != y_root:
#按秩合并
if self.rank[x_root] < self.rank[y_root]:
self.parent[x_root] = y_root
elif self.rank[x_root] > self.rank[y_root]:
self.parent[y_root] = x_root
else:
self.parent[y_root] = x_root
self.rank[x_root] += 1
self.count -= 1
# 测试代码
if __name__ == "__main__":
uf = UnionFind(9)
uf.union(0, 2)
uf.union(2, 3)
uf.union(1, 3)
uf.union(4, 3)
uf.union(5, 6)
uf.union(7, 6)
print("并查集中有 {} 个集合".format(uf.count))
if uf.find(0) == uf.find(4):
print("0和4在同一个集合里")
else:
print("0和4不在同一个集合里")
if uf.find(8) == uf.find(5):
print("8和5在同一个集合里")
else:
print("8和5不在同一个集合里")
程序的运行结果为:
并查集中有 3 个集合
0和4在同一个集合里
8和5不在同一个集合里
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: