高精度除法详解(C++实现,图文并茂)
在科学计算中经常会有几十位、几百位的大数,这类数被统称为“高精度数”。
高精度算法是处理高精度数的数学计算方法,它是用计算机对高精度数模拟加、减、乘、除、乘方、阶乘、开方等运算的算法。
受到存储精度的限制,在计算机中无法正常存储非常大的数。这时可以将非常大的数按照一位或者四位进行拆分,将其存储在一个数组中,用一个数组表示这个数字。
高精度除法分为高精度数除以单精度数和高精度数除以高精度数两种,入门级只要求掌握高精度数除以单精度数的方法即可。
高精度除法的原理是,以字符串的形式接收高精度数,将其转换为数字后正序存储在数组中,从高位到低位模拟高精度除法运算。在进行除法运算时,需要从高位到低位进行处理,没有进位问题,因此采用正序存储,数组头部存储高精度数的高位。
例如,用字符串接收 s1="129786",将其正序存储在一维数组 a[] 中:

例如,求解 129786/15,过程如下:
1) 将高精度数正序存储在数组 a[] 中,单精度数 b=15。
2) 从高位到低位依次处理每位数字,将结果存储在数组 c[] 中。

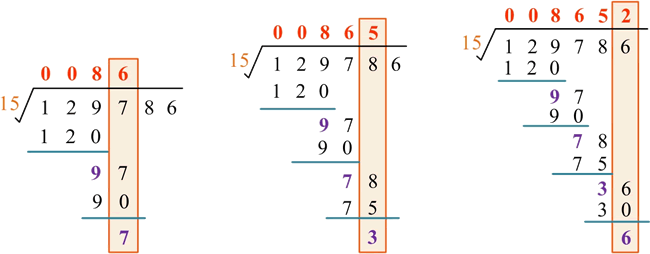
3) 删除前导 0,从高位到低位依次输出答案 8652,即 129786/15=8652。
2) 从高位到低位依次处理每位数字,按位相除,将上次的余数 ×10 +当前位作为被除数,进行除法运算,记录商和余数。
3) 在除法运算结果中有可能高位出现多个前导 0,删除前导 0,从高位到低位依次输出答案。
高精度算法是处理高精度数的数学计算方法,它是用计算机对高精度数模拟加、减、乘、除、乘方、阶乘、开方等运算的算法。
受到存储精度的限制,在计算机中无法正常存储非常大的数。这时可以将非常大的数按照一位或者四位进行拆分,将其存储在一个数组中,用一个数组表示这个数字。
高精度除法分为高精度数除以单精度数和高精度数除以高精度数两种,入门级只要求掌握高精度数除以单精度数的方法即可。
高精度除法的原理是,以字符串的形式接收高精度数,将其转换为数字后正序存储在数组中,从高位到低位模拟高精度除法运算。在进行除法运算时,需要从高位到低位进行处理,没有进位问题,因此采用正序存储,数组头部存储高精度数的高位。
例如,用字符串接收 s1="129786",将其正序存储在一维数组 a[] 中:

高精度除法按位相除
在进行除法运算时,从高位到低位依次处理每位数字,将上次余数 ×10+当前位作为被除数,继续进行除法运算。按位相除,每次的商值范围均为 0~9。例如,求解 129786/15,过程如下:
1) 将高精度数正序存储在数组 a[] 中,单精度数 b=15。
2) 从高位到低位依次处理每位数字,将结果存储在数组 c[] 中。
- i=1:初始时,余数 x=0,x=x×10+a[1]=1,c[1]=x/15=0,更新余数 x,x=x%15=1。
- i=2:x=x×10+a[2]=12,c[2]=x/15=0,更新余数 x,x=x%15=12。
- i=3:x=x×10+a[3]=129,c[3]=x/15=8,更新余数 x,x=x%15=9。

- i=4:x=x×10+a[4]=97,c[4]=x/15=6,更新余数 x,x=x%15=7。
- i=5:x=x×10+a[5]=78,c[5]=x/15=5,更新余数 x,x=x%15=3。
- i=6:x=x×10+a[6]=36,c[6]=x/15=2,更新余数 x,x=x%15=6。

3) 删除前导 0,从高位到低位依次输出答案 8652,即 129786/15=8652。
高精度除法算法设计
1) 以字符串的形式接收被除数(高精度数),将其转换为数字后正序存储在数组 a[] 中,将除数(低精度数)存储在变量 b 中。2) 从高位到低位依次处理每位数字,按位相除,将上次的余数 ×10 +当前位作为被除数,进行除法运算,记录商和余数。
3) 在除法运算结果中有可能高位出现多个前导 0,删除前导 0,从高位到低位依次输出答案。
高精度除法算法实现
#include <iostream>
using namespace std;
const int maxn=10010;
int a[maxn],c[maxn];
int main(){
string s; // 被除数
long long b,x=0; // 除数,累加余数时要乘以10,不能定义为int类型
cin>>s>>b;
int n=s.length();
for(int i=0;i<n;i++) // 将第1个字符串存储在数组中,正序存储
a[i+1]=s[i]-'0';
for(int i=1;i<=n;i++){ // 除法运算
x=x*10+a[i]; // 累加上次的余数和当前位
c[i]=x/b; // 记录商
x%=b; // 更新余数
}
int lenc=1;
while(c[lenc]==0&&lenc<n) lenc++; // 删除前导0
for(int i=lenc;i<=n;i++) // 从高位到低位依次输出答案
cout<<c[i];
return 0;
}
运行结果为:
129786 15
8652
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: