高精度加法讲解(图文并茂,C++实现)
在科学计算中经常会有几十位、几百位的大数,这类数被统称为“高精度数”。
高精度算法是处理高精度数的数学计算方法,它是用计算机对高精度数模拟加、减、乘、除、乘方、阶乘、开方等运算的算法。
高精度加法的原理是,以字符串的形式接收高精度数,将其转换为数字后逆序存储在数组中,从低位到高位模拟高精度加法运算。
例如,用字符串接收高精度数 s1=“93825456”,将其逆序存储在一维数组 a[] 中:

例如,求解 93825456+8542639,步骤如下:
1) 将两个数分别逆序存储在数组 a[]、b[] 中:
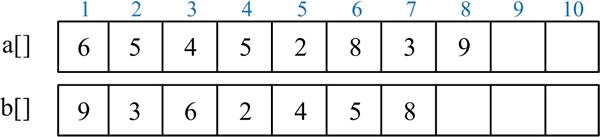
2) 从低位到高位依次处理每位数字,将结果存储在数组 c[] 中:
处理第 1 位:初始时,c[1]=0。c[1] 累加当前位的数字,c[1]=c[1]+a[1]+b[1]=0+6+9=15,c[1]=15%10=5,将进位存入 c[2],c[2]=15/10=1:
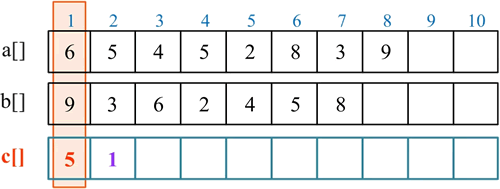
处理第 2 位:c[2] 累加当前位的数字,c[2]=c[2]+a[2]+b[2]=1+5+3=9,c[2]=9%10=9,将进位存入 c[3],c[3]=9/10=0:
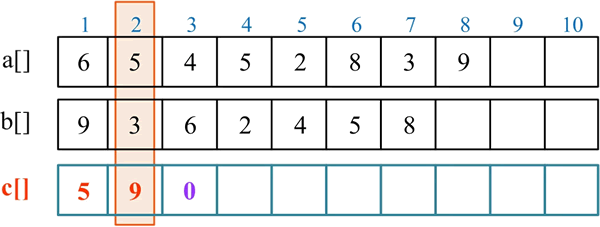
处理第 3 位:c[3] 累加当前位的数字,c[3]=c[3]+a[3]+b[3]=0+6+4=10,c[3]=10%10=0,将进位存入 c[4],c[4]=10/10=1:
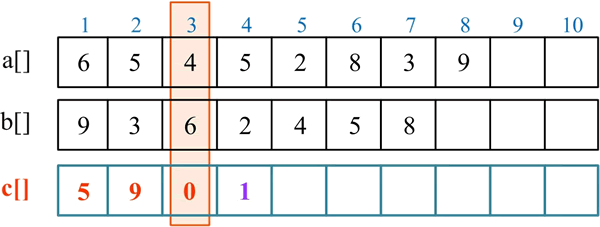
处理第 4 位:c[4] 累加当前位的数字,c[4]=c[4]+a[4]+b[4]=1+5+2=8,c[4]=8%10=8,将进位存入 c[5],c[5]=8/10=0:
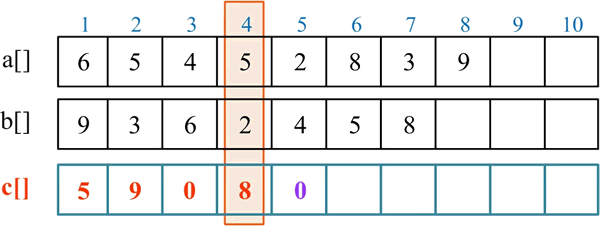
处理第 5 位:c[5] 累加当前位的数字,c[5]=c[5]+a[5]+b[5]=0+2+4=6,c[5]=6%10=6,将进位存入 c[6],c[6]=6/10=0:
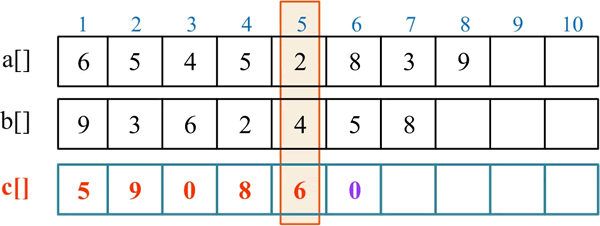
处理第 6 位:c[6] 累加当前位的数字,c[6]=c[6]+a[6]+b[6]=0+8+5=13,c[6]=13%10=3,将进位存入 c[7],c[7]=13/10=1:

处理第 7 位:c[7] 累加当前位的数字,c[7]=c[7]+a[7]+b[7]=1+3+8=12,c[7]=12%10=2,将进位存入 c[8],c[8]=12/10=1:
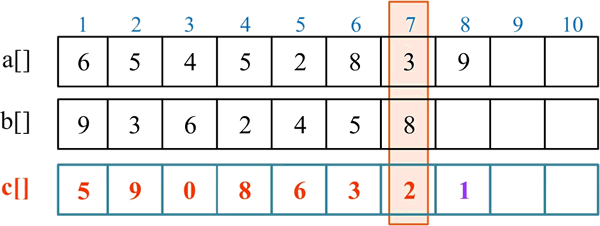
处理第 8 位:c[8] 累加当前位的数字,c[8]=c[8]+a[8]+b[8]=1+9+0=10,c[8]=10%10=0,将进位存入 c[9],c[9]=10/10=1:
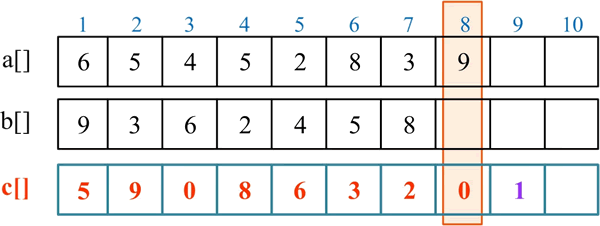
3) 处理完毕,从高位到低位依次输出答案 102368095,即 93825456+8542639=102368095。
高精度算法是处理高精度数的数学计算方法,它是用计算机对高精度数模拟加、减、乘、除、乘方、阶乘、开方等运算的算法。
高精度加法的原理是,以字符串的形式接收高精度数,将其转换为数字后逆序存储在数组中,从低位到高位模拟高精度加法运算。
接收和存储数据
在进行加法运算时可能会有进位,若将最高位存储在数组首部,则无法存储进位,因此采用逆序存储,在数组尾部存储高精度数的高位,这样可以将进位追加存储在数组尾部。例如,用字符串接收高精度数 s1=“93825456”,将其逆序存储在一维数组 a[] 中:

处理进位
在进行加法运算时,从低位到高位依次处理每位数字,若两个数的当前位与进位相加大于或等于 10,则向高位进位。例如,求解 93825456+8542639,步骤如下:
1) 将两个数分别逆序存储在数组 a[]、b[] 中:

2) 从低位到高位依次处理每位数字,将结果存储在数组 c[] 中:
处理第 1 位:初始时,c[1]=0。c[1] 累加当前位的数字,c[1]=c[1]+a[1]+b[1]=0+6+9=15,c[1]=15%10=5,将进位存入 c[2],c[2]=15/10=1:

处理第 2 位:c[2] 累加当前位的数字,c[2]=c[2]+a[2]+b[2]=1+5+3=9,c[2]=9%10=9,将进位存入 c[3],c[3]=9/10=0:

处理第 3 位:c[3] 累加当前位的数字,c[3]=c[3]+a[3]+b[3]=0+6+4=10,c[3]=10%10=0,将进位存入 c[4],c[4]=10/10=1:

处理第 4 位:c[4] 累加当前位的数字,c[4]=c[4]+a[4]+b[4]=1+5+2=8,c[4]=8%10=8,将进位存入 c[5],c[5]=8/10=0:

处理第 5 位:c[5] 累加当前位的数字,c[5]=c[5]+a[5]+b[5]=0+2+4=6,c[5]=6%10=6,将进位存入 c[6],c[6]=6/10=0:

处理第 6 位:c[6] 累加当前位的数字,c[6]=c[6]+a[6]+b[6]=0+8+5=13,c[6]=13%10=3,将进位存入 c[7],c[7]=13/10=1:

处理第 7 位:c[7] 累加当前位的数字,c[7]=c[7]+a[7]+b[7]=1+3+8=12,c[7]=12%10=2,将进位存入 c[8],c[8]=12/10=1:

处理第 8 位:c[8] 累加当前位的数字,c[8]=c[8]+a[8]+b[8]=1+9+0=10,c[8]=10%10=0,将进位存入 c[9],c[9]=10/10=1:

3) 处理完毕,从高位到低位依次输出答案 102368095,即 93825456+8542639=102368095。
C++实现高精度加法
#include <iostream>
#include <string>
using namespace std;
int a[520], b[520], c[520];
int main() {
string s1, s2;
cin >> s1 >> s2;
int n = s1.length();
int m = s2.length();
int len = max(n, m); // 两个字符串的最大长度
for (int i = 0; i < n; i++) // 将第1个字符串存储在数组中,逆序存储
a[n - i] = s1[i] - '0';
for (int i = 0; i < m; i++) // 将第2个字符串存储在数组中,逆序存储
b[m - i] = s2[i] - '0';
for (int i = 1; i <= len; i++) { // 高精度加法
c[i] += a[i] + b[i]; // 累加
c[i + 1] = c[i] / 10; // 进位
c[i] %= 10; // 当前位
}
if (c[len + 1]) // 判断最后的进位是否为1
len++;
for (int i = len; i >= 1; i--) // 输出结果
cout << c[i];
return 0;
}
运行结果为:
93825456
8542639
102368095
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: