图的DFS深度优先遍历(图文并茂,C++实现)
图的遍历指从图的某一节点出发,按照某种搜索方式对图中的所有节点都访问且仅访问一次。
图的遍历可以解决很多搜索问题,实际应用非常广泛,根据搜索方式的不同,分为广度优先搜索(Breadth First Search,BFS)和深度优先搜索(Depth First Search,DFS)。
深度优先搜索是最常见的图搜索方式之一,指的是沿着一条路径一直搜索下去,在无法搜索时,回退到刚刚访问过的节点。
深度优先遍历指的是按照深度优先搜索方式对图进行遍历,实现的核心思路是:后被访问的节点,其邻接点先被访问。
根据深度优先遍历秘籍,后来先服务,可以借助栈实现。递归本身就是使用栈实现的,因此使用递归算法更方便。
例如,一个无向图如下图所示,其深度优先遍历的过程如下所述:
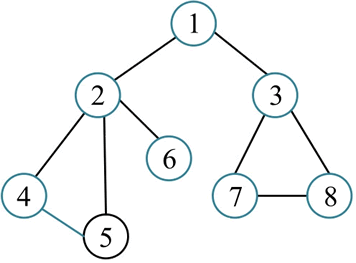
1) 初始化所有节点均未被访问,visited[i]=false,i=1,2,…,8。
2) 从 1 出发,将其标记为已访问,visited[1]=true。
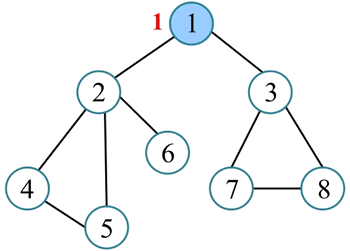
3) 从 1 出发访问其邻接点 2,从 2 出发访问其邻接点 4,从 4 出发访问其邻接点 5,5 没有未被访问的邻接点。
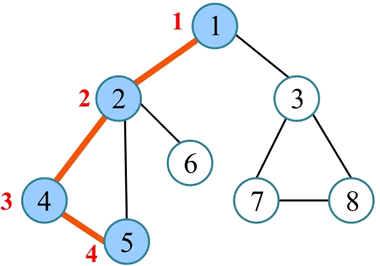
4) 回退到刚刚访问过的 4,4 也没有未被访问的邻接点,回退到最近访问过的 2,从 2 出发访问下一个未被访问的邻接点 6。
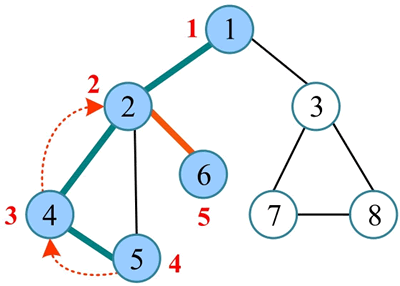
5) 6 没有未被访问的邻接点,回退到刚刚访问过的 2,2 没有未被访问的邻接点,回退到最近访问过的 1。
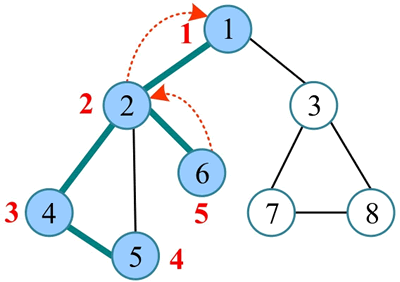
6) 从 1 出发访问下一个未被访问的邻接点 3,从 3 出发访问其邻接点 7,从 7 出发访问其邻接点 8,8 没有未被访问的邻接点。
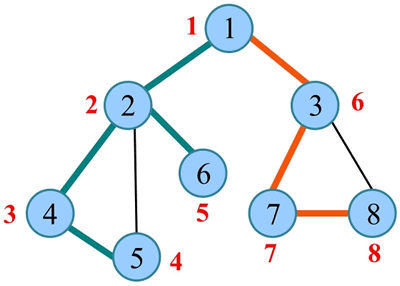
7) 回退到刚刚访问过的 7,7 也没有未被访问的邻接点,回退到最近访问过的 3,3 也没有未被访问的邻接点,回退到最近访问过的 1,1 也没有未被访问的邻接点,遍历结束。
深度优先遍历序列为 1 2 4 5 6 3 7 8,如下图所示:
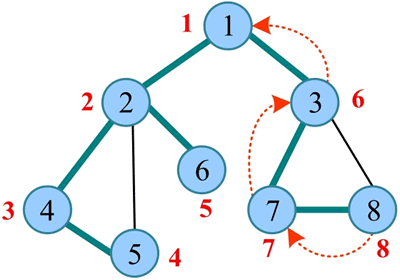
深度优先遍历经过的节点及边形成的树被称为“深度优先生成树”,如下图所示。

若深度优先遍历非连通图,则每个连通分量都会产生一棵深度优先生成树,所有深度优先生成树构成深度优先生成森林。
2) 基于链式前向星的深度优先遍历:
3) 对非连通图进行深度优先遍历时,从某个节点 s 出发可能无法遍历所有节点,需要查漏补缺,检查每个节点,若某个节点未被访问,则从该节点出发进行深度优先遍历。
1) 基于邻接矩阵的深度优先遍历算法。遍历每个节点的邻接点的时间复杂度为 O(n),共 n 个节点,总时间复杂度为 O(n^2)。使用了一个递归工作栈,空间复杂度为 O(n)。
2) 基于邻接表的深度优先遍历算法。遍历节点 vi 的邻接点的时间复杂度为 O(d(vi)),d(vi) 为 vi 的度,有向图所有节点的出度之和等于边数 e;无向图所有节点的度之和等于 2e,因此遍历所有邻接点的时间复杂度为 O(e),访问所有节点的时间复杂度为 O(n),总时间复杂度为 O(n+e)。使用了一个递归工作栈,空间复杂度为 O(n)。
注意 一个图的邻接矩阵是唯一的,因此基于邻接矩阵的广度优先遍历序列或深度优先遍历序列也是唯一的,而图的邻接表不是唯一的,边的输入顺序不同,正序或逆序建表都会影响邻接表中的邻接点顺序,因此基于邻接表的广度优先遍历序列或深度优先遍历序列不是唯一的。
图的遍历可以解决很多搜索问题,实际应用非常广泛,根据搜索方式的不同,分为广度优先搜索(Breadth First Search,BFS)和深度优先搜索(Depth First Search,DFS)。
深度优先搜索是最常见的图搜索方式之一,指的是沿着一条路径一直搜索下去,在无法搜索时,回退到刚刚访问过的节点。
深度优先遍历指的是按照深度优先搜索方式对图进行遍历,实现的核心思路是:后被访问的节点,其邻接点先被访问。
根据深度优先遍历秘籍,后来先服务,可以借助栈实现。递归本身就是使用栈实现的,因此使用递归算法更方便。
深度优先遍历的实现过程
- 初始化图中的所有节点均未被访问。
- 从图中的某个节点u出发,访问 u 并将其标记为已访问。
- 依次检查 u 的所有邻接点 v,若 v 未被访问,则从 v 出发进行深度优先遍历。
例如,一个无向图如下图所示,其深度优先遍历的过程如下所述:

1) 初始化所有节点均未被访问,visited[i]=false,i=1,2,…,8。
2) 从 1 出发,将其标记为已访问,visited[1]=true。

3) 从 1 出发访问其邻接点 2,从 2 出发访问其邻接点 4,从 4 出发访问其邻接点 5,5 没有未被访问的邻接点。

4) 回退到刚刚访问过的 4,4 也没有未被访问的邻接点,回退到最近访问过的 2,从 2 出发访问下一个未被访问的邻接点 6。

5) 6 没有未被访问的邻接点,回退到刚刚访问过的 2,2 没有未被访问的邻接点,回退到最近访问过的 1。

6) 从 1 出发访问下一个未被访问的邻接点 3,从 3 出发访问其邻接点 7,从 7 出发访问其邻接点 8,8 没有未被访问的邻接点。

7) 回退到刚刚访问过的 7,7 也没有未被访问的邻接点,回退到最近访问过的 3,3 也没有未被访问的邻接点,回退到最近访问过的 1,1 也没有未被访问的邻接点,遍历结束。
深度优先遍历序列为 1 2 4 5 6 3 7 8,如下图所示:

深度优先遍历经过的节点及边形成的树被称为“深度优先生成树”,如下图所示。

若深度优先遍历非连通图,则每个连通分量都会产生一棵深度优先生成树,所有深度优先生成树构成深度优先生成森林。
深度优先遍历算法的具体实现
1) 基于邻接矩阵的深度优先遍历:
void DFS_AM(int u) { // 基于邻接矩阵的深度优先遍历
cout<<u<<"\t";
visited[u]=true;
for (int v=1;v<=n;v++) { // 依次检查所有节点
if (G[u][v] && !visited[v]) // u、v 邻接而且 v 未被访问
DFS_AM(v); // 从 v 开始进行递归深度优先遍历
}
}
2) 基于链式前向星的深度优先遍历:
void DFS_ListGraph(int u) { // 基于链式前向星的深度优先遍历
cout << u << "\t";
visited[u] = true;
for (int i = head[u]; ~i; i = e[i].next) { // 依次检查 u 的所有邻接点,i != -1 可以写为 ~i
int v = e[i].to; // u 的邻接点 v
if (!visited[v]) { // v 未被访问
DFS_ListGraph(v); // 从 v 开始进行递归深度优先遍历
}
}
}
3) 对非连通图进行深度优先遍历时,从某个节点 s 出发可能无法遍历所有节点,需要查漏补缺,检查每个节点,若某个节点未被访问,则从该节点出发进行深度优先遍历。
void DFS() { // 非连通图的深度优先遍历
for (int v = 1; v <= n; v++) // 对非连通图需要查漏补缺,检查未被访问的节点
if (!visited[v]) // v 未被访问,以 v 为起点再次进行深度优先遍历
DFS_AM(v);
}
深度优先遍历算法分析
深度优先遍历是对每个节点都遍历其邻接点的过程,图的存储方式不同,其算法复杂度也不同。1) 基于邻接矩阵的深度优先遍历算法。遍历每个节点的邻接点的时间复杂度为 O(n),共 n 个节点,总时间复杂度为 O(n^2)。使用了一个递归工作栈,空间复杂度为 O(n)。
2) 基于邻接表的深度优先遍历算法。遍历节点 vi 的邻接点的时间复杂度为 O(d(vi)),d(vi) 为 vi 的度,有向图所有节点的出度之和等于边数 e;无向图所有节点的度之和等于 2e,因此遍历所有邻接点的时间复杂度为 O(e),访问所有节点的时间复杂度为 O(n),总时间复杂度为 O(n+e)。使用了一个递归工作栈,空间复杂度为 O(n)。
注意 一个图的邻接矩阵是唯一的,因此基于邻接矩阵的广度优先遍历序列或深度优先遍历序列也是唯一的,而图的邻接表不是唯一的,边的输入顺序不同,正序或逆序建表都会影响邻接表中的邻接点顺序,因此基于邻接表的广度优先遍历序列或深度优先遍历序列不是唯一的。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: