图的BFS广度优先遍历(图文并茂,C++实现)
图的遍历指从图的某一节点出发,按照某种搜索方式对图中的所有节点都访问且仅访问一次。
图的遍历可以解决很多搜索问题,实际应用非常广泛,根据搜索方式的不同,分为广度优先搜索(Breadth First Search,BFS)和深度优先搜索(Depth First Search,DFS)。
广度优先搜索指从某个节点(源点)出发,一次性访问所有未被访问的邻接点,再依次从这些已访问过的邻接点出发,一层一层地访问,如下图所示。广度优先遍历指按照广度优先搜索方式对图进行遍历。
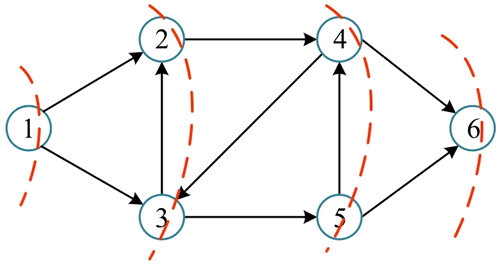
假设源点为 1,从 1 出发访问 1 的邻接点 2、3,从 2 出发访问 4,从 3 出发访问 5,从 4 出发访问 6,访问完毕。访问路径如下图所示:
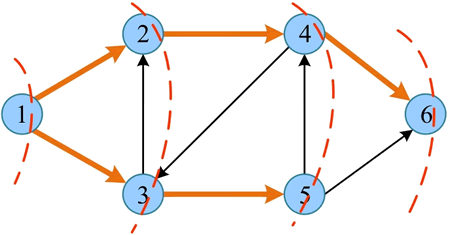
广度优先遍历的实现思路是:先被访问的节点,其邻接点先被访问,可以借助队列实现。
因为对每个节点都访问且仅访问一次,所以设置一个辅助数组 visited[]。visited[i]=false,表示节点 i 未被访问;visited[i]=true,表示节点 i 已被访问。
广度优先遍历的算法步骤是:
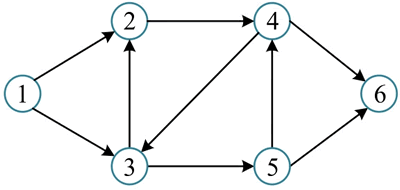
1) 初始化 visited[i]=false,i=1,2,…,6。并初始化一个空队列 Q。
2) 从 1 出发,将其标记为已访问,visited[1]=true,将 1 入队。
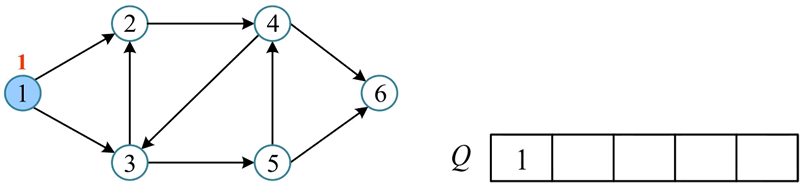
3) 将队头元素1出队,访问1未被访问的邻接点 2、3,将其标记为已访问并入队。
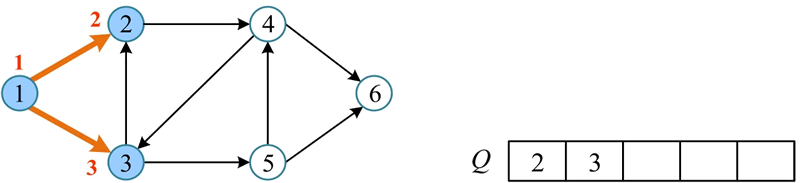
4) 将队头元素 2 出队,将 2 未被访问的邻接点 4 标记为已访问并入队。
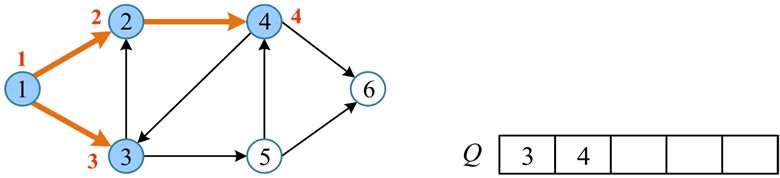
5) 将队头元素 3 出队,3 的邻接点 2 已被访问,将 3 未被访问的邻接点 5 标记为已访问并入队。
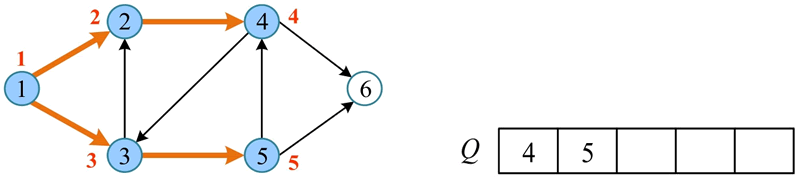
6) 将队头元素 4 出队,4 的邻接点 3 已被访问,将 4 未被访问的邻接点 6 标记为已访问并入队。

7) 将队头元素 5 出队,5 的邻接点 4、6 均已被访问,没有未被访问的邻接点。
8) 将队头元素 6 出队,6 没有邻接点。
9) 队列为空,算法结束。广度优先遍历序列为
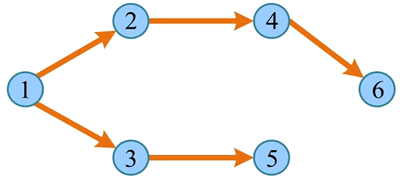
广度优先遍历经过的节点及边形成的树被称为“广度优先生成树”,如下图所示。若广度优先遍历非连通图,则每个连通分量都会产生一棵广度优先生成树,所有广度优先生成树构成广度优先生成森林。
2) 基于链式前向星的广度优先遍历:
3) 对非连通图进行广度优先遍历时,从某一个节点 s 出发,可能无法遍历所有节点,需要查漏补缺,检查每个节点,若未被访问,则从该节点出发进行广度优先遍历:
1) 基于邻接矩阵的广度优先遍历。遍历每个节点的邻接点的时间复杂度为 O(n),共 n 个节点,总时间复杂度为 O(n^2)。使用了一个辅助队列,每个节点都只入队一次,空间复杂度为 O(n)。
2) 基于邻接表的广度优先遍历。遍历节点 vi 的邻接点的时间复杂度为 O(d(vi)),d(vi)为 vi 的度,有向图中所有节点的出度之和等于边数 e;无向图中所有节点的度之和等于 2e,因此遍历所有邻接点的时间复杂度为 O(e),访问所有节点的时间复杂度为 O(n),总时间复杂度为 O(n+e)。使用了一个辅助队列,每个节点都只入队一次,空间复杂度为 O(n)。
图的遍历可以解决很多搜索问题,实际应用非常广泛,根据搜索方式的不同,分为广度优先搜索(Breadth First Search,BFS)和深度优先搜索(Depth First Search,DFS)。
图的广度优先遍历
广度优先搜索又被称为“宽度优先搜索”,是最常见的图搜索方式之一。广度优先搜索指从某个节点(源点)出发,一次性访问所有未被访问的邻接点,再依次从这些已访问过的邻接点出发,一层一层地访问,如下图所示。广度优先遍历指按照广度优先搜索方式对图进行遍历。

假设源点为 1,从 1 出发访问 1 的邻接点 2、3,从 2 出发访问 4,从 3 出发访问 5,从 4 出发访问 6,访问完毕。访问路径如下图所示:

广度优先遍历的实现思路是:先被访问的节点,其邻接点先被访问,可以借助队列实现。
因为对每个节点都访问且仅访问一次,所以设置一个辅助数组 visited[]。visited[i]=false,表示节点 i 未被访问;visited[i]=true,表示节点 i 已被访问。
广度优先遍历的算法步骤是:
- 初始化 visited[i]=false,i=1,2,…,n,表示所有节点均未被访问,并初始化一个空队列。
- 从图中的某个节点v出发,访问 v 并将其标记为已访问,将 v 入队。
- 若队列不为空,则继续执行,否则算法结束。
- 将队头元素 v 出队,访问 v 所有未被访问的邻接点,将其标记为已访问并入队。转向第 3 步。
广度优先遍历完美图解
例如,一个有向图如下图所示,其广度优先遍历的过程如下所述。
1) 初始化 visited[i]=false,i=1,2,…,6。并初始化一个空队列 Q。
2) 从 1 出发,将其标记为已访问,visited[1]=true,将 1 入队。

3) 将队头元素1出队,访问1未被访问的邻接点 2、3,将其标记为已访问并入队。

4) 将队头元素 2 出队,将 2 未被访问的邻接点 4 标记为已访问并入队。

5) 将队头元素 3 出队,3 的邻接点 2 已被访问,将 3 未被访问的邻接点 5 标记为已访问并入队。

6) 将队头元素 4 出队,4 的邻接点 3 已被访问,将 4 未被访问的邻接点 6 标记为已访问并入队。

7) 将队头元素 5 出队,5 的邻接点 4、6 均已被访问,没有未被访问的邻接点。
8) 将队头元素 6 出队,6 没有邻接点。
9) 队列为空,算法结束。广度优先遍历序列为
1 2 3 4 5 6。广度优先遍历经过的节点及边形成的树被称为“广度优先生成树”,如下图所示。若广度优先遍历非连通图,则每个连通分量都会产生一棵广度优先生成树,所有广度优先生成树构成广度优先生成森林。

广度优先遍历算法实现
1) 基于邻接矩阵的广度优先遍历:
void BFS_AM(int s) { // 基于邻接矩阵的广度优先遍历
queue<int> Q; // 创建一个普通队列(先进先出),存储 int 类型的数据
cout<<s<<"\t";
visited[s]=true; // 标记为已访问
Q.push(s); // 将 s 入队
while (!Q.empty()) { // 若队列不为空
int u=Q.front(); // 取出队头元素
Q.pop(); // 队头元素出队
for(int v=1;v<=n;v++) { // 依次检查所有节点
if (G[u][v] && !visited[v]) { // u、v 邻接而且 v 未被访问
cout<<v<<"\t";
visited[v]=true;
Q.push(v);
}
}
}
}
2) 基于链式前向星的广度优先遍历:
void BFS_ListGraph(int s) { // 基于链式前向星的广度优先遍历
queue<int> Q; // 创建一个普通队列(先进先出),存储 int 类型的数据
cout<<s<<"\t";
visited[s]=true; // 标记为已访问
Q.push(s); // 将 s 入队
while (!Q.empty()) { // 若队列不为空
int u=Q.front(); // 取出队头元素
Q.pop(); // 队头元素出队
for(int i=head[u];~i;i!=e[i].next) { // 依次检查 u 的所有邻接点,i!=-1 可以写为~i
int v=e[i].to; // u 的邻接点 v
if (!visited[v]) { // v 未被访问
cout<<v<<"\t";
visited[v]=true;
Q.push(v);
}
}
}
}
3) 对非连通图进行广度优先遍历时,从某一个节点 s 出发,可能无法遍历所有节点,需要查漏补缺,检查每个节点,若未被访问,则从该节点出发进行广度优先遍历:
void BFS() { // 非连通图的广度优先遍历
for (int v=1; v<=n; v++) // 对非连通图需要查漏补缺,检查未被访问的节点
if (!visited[v]) // v 未被访问,以 v 为起点再次进行广度优先遍历
BFS_AM(v);
}
广度优先遍历算法分析
广度优先遍历是对每个节点都遍历其邻接点的过程,图的存储方式不同,其算法复杂度也不同。1) 基于邻接矩阵的广度优先遍历。遍历每个节点的邻接点的时间复杂度为 O(n),共 n 个节点,总时间复杂度为 O(n^2)。使用了一个辅助队列,每个节点都只入队一次,空间复杂度为 O(n)。
2) 基于邻接表的广度优先遍历。遍历节点 vi 的邻接点的时间复杂度为 O(d(vi)),d(vi)为 vi 的度,有向图中所有节点的出度之和等于边数 e;无向图中所有节点的度之和等于 2e,因此遍历所有邻接点的时间复杂度为 O(e),访问所有节点的时间复杂度为 O(n),总时间复杂度为 O(n+e)。使用了一个辅助队列,每个节点都只入队一次,空间复杂度为 O(n)。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: