MATLAB矩阵运算(快速入门)
矩阵的基本运算包括加、减、乘、数乘、点乘、乘方、左除、右除等。其中,加、减、乘与大家所学的线性代数中的对应运算是一样的,相应的运算符为“+”、“-” 和 “*”。
对于上述的四则运算,需要注意的是:矩阵的加、减、乘运算的维数要求与线性代数中的要求一致。
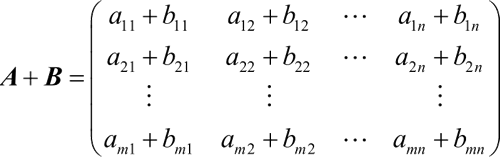
矩阵的加法运算符合如下规律:
【实例】验证加法法则。
MATLAB 程序如下:
减法运算法则为:A-B=A+(-B)。
【实例】矩阵求和。
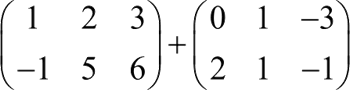
MATLAB 程序如下:
【实例】矩阵求差。
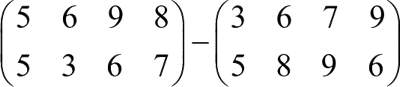
MATLAB 程序如下:
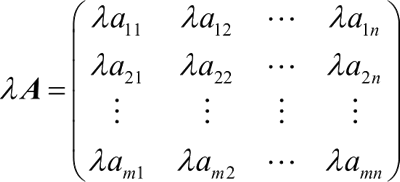
矩阵的数乘运算满足下面的规律:
矩阵的乘法需要满足:矩阵 A 的列数与矩阵 B 的行数相同。
矩阵 A 乘以矩阵 B 的积矩阵 C 具有以下特点:
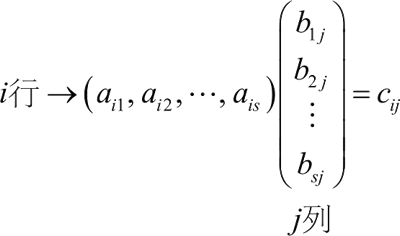
例如:
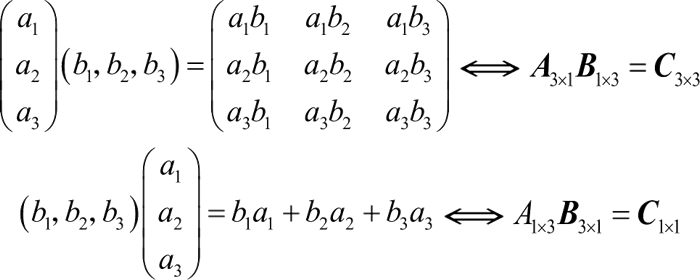
所以,若矩阵 A、B 满足 AB=0,未必有 A=0 或 B=0 的结论。
【实例】矩阵乘法运算。
MATLAB 程序如下:
对于线性方程组 DX=B,如果 D 非奇异,即它的逆矩阵存在,则用 MATLAB 对其求解的结果为:
左除的条件:B 的行数等于 D 的阶数(D 的行数和列数相同,简称阶数)。
【实例】求解矩阵左除。
右除的条件:B1 的列数等于 D1 的阶数(D1 的行数和列数相同,简称阶数)。
【实例】验证矩阵右除。
MATLAB 程序如下:
对于上述的四则运算,需要注意的是:矩阵的加、减、乘运算的维数要求与线性代数中的要求一致。
矩阵的加减运算
设 A =(aij),B =(bij) 都是 m×n 矩阵,矩阵 A 与 B 的和记成 A+B,规定为: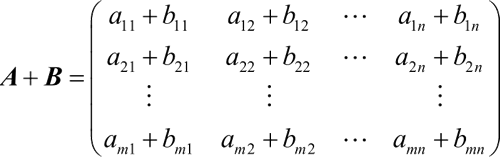
矩阵的加法运算符合如下规律:
- 交换律:A+B=B+A;
- 结合律:(A+B)+C=A+(B+C)。
【实例】验证加法法则。
MATLAB 程序如下:
>> clear % 清除工作区的变量
>> A=[5,6,9,8;5,3,6,7] % 创建矩阵A
A =
5 6 9 8
5 3 6 7
>> B=[3,6,7,9;5,8,9,6] % 创建矩阵B
B =
3 6 7 9
5 8 9 6
>> C=[9,3,5,6;8,5,2,1] % 创建矩阵C
C =
9 3 5 6
8 5 2 1
>> A+B % 矩阵B、A求和
ans =
8 12 16 17
10 11 15 13
>> B+A % 矩阵B、A求和,验证交换律
ans =
8 12 16 17
10 11 15 13
>> (A+B)+C % 矩阵A、B、C求和
ans =
17 15 21 23
18 16 17 14
>> A+(B+C) % 将矩阵A与矩阵B、C的和求和,验证结合律
ans =
17 15 21 23
18 16 17 14
>> D=[1,5,6;2,5,6] % 创建矩阵D
D =
1 5 6
2 5 6
>> A+D
矩阵维度必须一致。 % 只有相同维度的矩阵才能进行加法运算
减法运算法则为:A-B=A+(-B)。
【实例】矩阵求和。
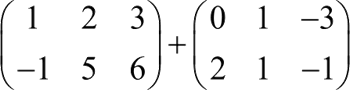
MATLAB 程序如下:
>> clear % 清除工作区的变量
>> [1 2 3;-1 5 6]+[0 1 -3;2 1 -1] % 直接输入两个矩阵求和
ans =
1 3 0
1 6 5
【实例】矩阵求差。
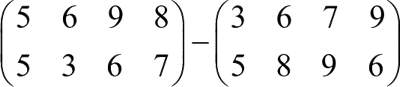
MATLAB 程序如下:
>> clear % 清除工作区的变量
>> A=[5,6,9,8;5,3,6,7]; % 创建矩阵A
>> B=[3,6,7,9;5,8,9,6]; % 创建矩阵B
>> -B % 计算-B
ans =
-3 -6 -7 -9
-5 -8 -9 -6
>> A-B % 两个矩阵求差
ans =
2 0 2 -1
0 -5 -3 1
矩阵的乘法运算
1) 数乘运算
数 λ 与矩阵 A=(aij)m×n 的乘积记成 λA 或 Aλ,规定为: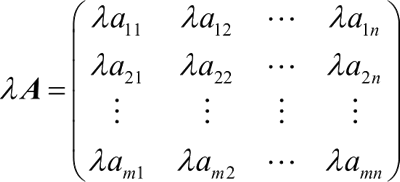
矩阵的数乘运算满足下面的规律:
λ(µA) = (λµ)A (λ+µ)A = λA+µA λ(A+B) = λA+λB其中,λ,μ 为实数,A,B 为矩阵。
>> clear % 清除工作区的变量
>> A=[1 2 3;0 3 3;7 9 5]; % 创建矩阵A
>> A*5 % 计算矩阵A与数值5的乘积
ans =
5 10 15
0 15 15
35 45 25
2) 乘运算
设 A=(aij) 是一个 m×s 矩阵,B=(bij) 是一个 s×n 矩阵,规定 A 与 B 的积为一个 m×n 矩阵 C=(cij)。其中,cij=ai1b1j+ai2b2j+…+aisbsj,i=1,2,…,m,j=1,2,…,n。矩阵的乘法需要满足:矩阵 A 的列数与矩阵 B 的行数相同。
矩阵 A 乘以矩阵 B 的积矩阵 C 具有以下特点:
- 积矩阵 C 的行数等于矩阵 A 的行数,积矩阵 C 的列数等于矩阵 B 的列数。
- 积矩阵 C 的第 i 行 j 列元素值等于矩阵 A 的 i 行元素与矩阵 B 的 j 列元素对应值积的和,即:
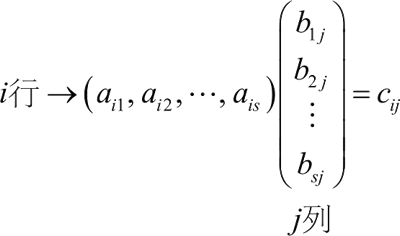
例如:
>> clear % 清除工作区的变量 >> A=[1 2 3;0 3 3;7 9 5]; % 创建矩阵A >> B=[8 3 9;2 8 1;3 9 1]; % 创建矩阵B >> A*B % 计算矩阵A、B的乘积 ans = 21 46 14 15 51 6 89 138 77
最后需要特别强调的是,由于:注意,AB≠BA,即矩阵的乘法不满足交换律。
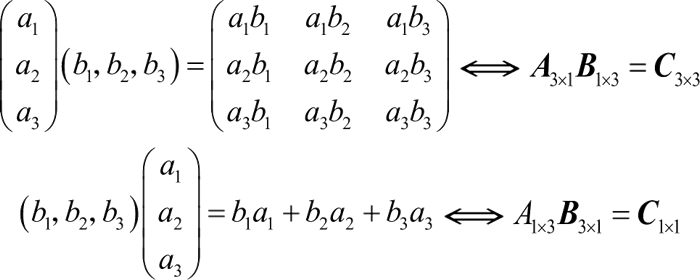
所以,若矩阵 A、B 满足 AB=0,未必有 A=0 或 B=0 的结论。
3) 点乘运算
点乘运算指将两矩阵中相同位置的元素进行相乘运算,将积保存在原位置组成新矩阵。例如:
>> clear
>> A=[1 2 3;0 3 3;7 9 5];
>> B=[8 3 9;2 8 1;3 9 1];
>> A.*B
ans =
8 6 27
0 24 3
21 81 5
【实例】矩阵乘法运算。
MATLAB 程序如下:
>> clear % 清除工作区的变量
>> A=[0 0;1 1] % 创建矩阵A
A =
0 0
1 1
>> B=[1 0;2 0] % 创建矩阵B
B =
1 0
2 0
>> 6*A - 5*B % 计算数值与矩阵的乘积后求差
ans =
-5 0
-4 6
>> A*B-A % 计算矩阵A乘B的积与矩阵A的差
ans =
0 0
2 -1
>> B*A-A % 计算矩阵B乘A的积与矩阵A的差,验证矩阵的乘法不满足交换律
ans =
0 0
-1 -1
>> A.*B-A % 计算矩阵A点乘矩阵B的积与矩阵A的差
ans =
0 0
1 -1
矩阵的除法运算
计算左除 A\B 时,A 的行数要与 B 的行数一致,计算右除 A/B 时,A 的列数要与 B 的列数一致。1) 左除运算
由于矩阵的特殊性,AB 通常不等于 BA,除法也一样。因此除法要区分左除和右除。对于线性方程组 DX=B,如果 D 非奇异,即它的逆矩阵存在,则用 MATLAB 对其求解的结果为:
X=inv(D)*B=D\B
符号“\”称为左除,即分母放在左边。左除的条件:B 的行数等于 D 的阶数(D 的行数和列数相同,简称阶数)。
【实例】求解矩阵左除。
MATLAB 程序如下:
>> clear % 清除工作区的变量
>> A=[1 2 3;0 3 3;7 9 5]; % 创建矩阵A
>> B=[8 3 9;2 8 1;3 9 1]; % 创建矩阵B
>> A\B % 两个矩阵左除
ans =
2.1515 -2.2121 2.8485
-3.8485 2.7879 -5.1515
4.5152 -0.1212 5.4848
2) 右除运算
若方程组表为 XD1=B1,D1 非奇异,即它的逆阵 inv(D1) 存在,则用 MATLAB 对其求解的结果为:X=B1*inv(D1)=B1/D1
符号“/”称为右除。右除的条件:B1 的列数等于 D1 的阶数(D1 的行数和列数相同,简称阶数)。
【实例】验证矩阵右除。
MATLAB 程序如下:
>> clear % 清除工作区的变量
>> A=[1 2 3;5 8 6]; % 创建矩阵A
>> B=[8 6 9;4 3 7]; % 创建矩阵B
>> C=A/B % 两个矩阵右除
C =
-0.0400 0.4800
1.2640 -0.7680
3) 点除运算
所谓矩阵的点除运算,是指将两矩阵中相同位置的元素进行相除运算并将商保存在原位置组成新矩阵,具体如下:- 点左除:a.\b 表示矩阵 b 中的每个元素除以矩阵 a 对应位置的元素;
- 点右除:a./b 表示矩阵 a 中的每个元素除以矩阵 b 对应位置的元素。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: