最短路径算法
在给定的图存储结构中,从某一顶点到另一个顶点所经过的多条边称为路径。
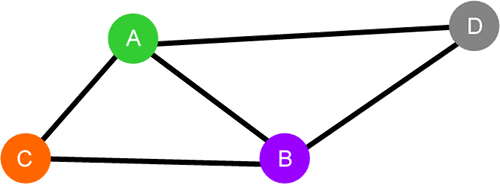
图 1 图存储结构
例如在图 1 所示的图结构中,从顶点 A 到 B 的路径有多条,包括 A-B、A-C-B 和 A-D-B。当我们给图中的每条边赋予相应的权值后,就可以从众多路径中找出总权值最小的一条,这条路径就称为最短路径。
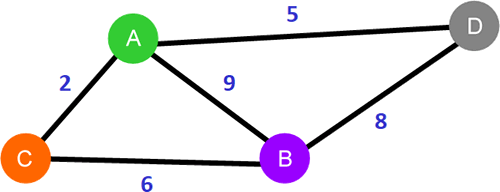
图 2 无向带权图
以图 2 为例,从顶点 A 到 B 的路径有 3 条,它们各自的总权值是:
最短路径不仅适用于无向加权图,也适用于有向加权图,如下图所示:
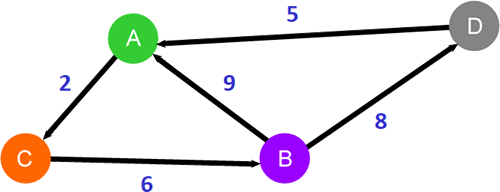
图 3 有向加权图
和图 2 相比,图 3 中的每条边都标有方向,以权值为 2 的边为例,它只表示从顶点 A 到 C 的一条边,而从顶点 C 是无法直达 A 的。从顶点 A 到 B 的路径仅有 1 条,就是 A->C->B,因此它自然也就是从 A 到 B 的最短路径。
常用的查找最短路径的算法有 4 种,下表给出了它们各自的名称和特点。

图 1 图存储结构
例如在图 1 所示的图结构中,从顶点 A 到 B 的路径有多条,包括 A-B、A-C-B 和 A-D-B。当我们给图中的每条边赋予相应的权值后,就可以从众多路径中找出总权值最小的一条,这条路径就称为最短路径。

图 2 无向带权图
以图 2 为例,从顶点 A 到 B 的路径有 3 条,它们各自的总权值是:
A-B:9
A-C-B:2+6=8
A-D-B:5+8=13
最短路径不仅适用于无向加权图,也适用于有向加权图,如下图所示:

图 3 有向加权图
和图 2 相比,图 3 中的每条边都标有方向,以权值为 2 的边为例,它只表示从顶点 A 到 C 的一条边,而从顶点 C 是无法直达 A 的。从顶点 A 到 B 的路径仅有 1 条,就是 A->C->B,因此它自然也就是从 A 到 B 的最短路径。
最短路径算法
实际生产和生活中,经常需要查找最短路径,例如借助高德、腾讯地图等导航工具查找到目的地的最短可行路线,建立道路交通网、物流运输网络、计算机网络等,这时就可以使用最短路径算法。常用的查找最短路径的算法有 4 种,下表给出了它们各自的名称和特点。
| 最短路径算法 | 描 述 |
|---|---|
| 迪杰斯特拉算法(Dijkstra) | 寻找某个特定顶点到其它所有顶点的最短路径,该算法要求所有路径的权值为非负数。 |
| 弗洛伊德算法(Floyd-Warshall) | 寻找各个顶点之间的最短路径,允许非环路的路径权值为负数,该算法不仅适用于稀疏图,在稠密图(路径数量多的图)中寻找最短路径的效率也很高。 |
| 贝尔曼福特算法(Bellman-Ford) |
寻找某个特定顶点到其它所有顶点的最短路径,该算法允许路径的权值为负数。 推荐阅读:
|
| 约翰逊算法(Johnson) |
寻找各个顶点之间的最短路径,允许非环路的路径权值为负数,该算法更适用于稀疏图(路径数量少的图)。 推荐阅读:
|
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: