归并排序算法(图文并茂,C++实现)
归并排序采用的是分治策略,将原问题分解为很多个子问题,先解决子问题,再通过子问题解决原问题。
可以先将待排序元素分解为两个规模大致相等的子序列,若不易解决,则继续分解子序列,直到子序列中的元素数量为 1。因为单个元素的序列本身是有序的,所以此时便可以进行合并,从而得到一个完整的有序序列。
归并排序算法步骤
从上图可以看出,首先将待排序元素分解为两个规模大致相等的子序列,然后分别把子序列分解为两个规模大致相等的子序列,如此下去,直到子序列中只剩一个元素时为止,这时含有一个元素的子序列就是有序的。
然后将两个有序子序列合并为一个有序序列,如此下去,直到所有元素都被合并为一个有序序列时为止。

为实现合并操作,设置三个变量 i、j、k 和一个辅助数组 b[]:
比较 a[i] 和 a[j],将较小的赋值给 b[k],同时将相应的变量向后移动。如此下去,直到将所有元素都处理完毕。最后将辅助数组中已排好序的元素复制到原数组 a[] 中,如下图所示。
第 1 次比较,a[i]=4,a[j]=2,将较小的元素 2 放入辅助数组 b[],j++,k++。
第 2 次比较,a[i]=4,a[j]=6,将较小的元素 4 放入辅助数组 b[],i++,k++。
第 3 次比较,a[i]=9,a[j]=6,将较小的元素 6 放入辅助数组 b[],j++,k++。
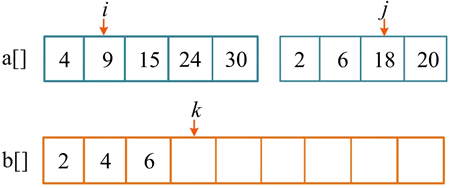
第 4 次比较,a[i]=9,a[j]=18,将较小的元素 9 放入辅助数组 b[],i++,k++。
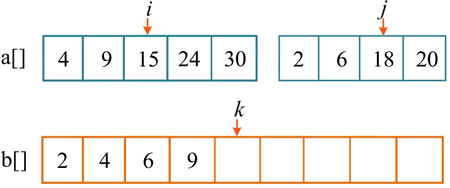
第 5 次比较,a[i]=15,a[j]=18,将较小的元素 15 放入辅助数组 b[],i++,k++。
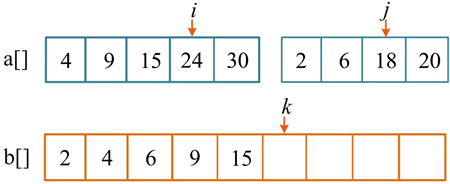
第 6 次比较,a[i]=24,a[j]=18,将较小的元素 18 放入辅助数组 b[],j++,k++。
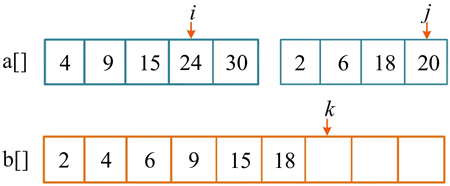
第 7 次比较,a[i]=24,a[j]=20,将较小的元素 20 放入辅助数组 b[],j++,k++。
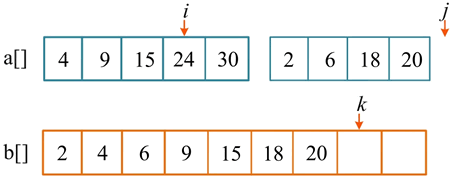
此时,j>right,后半部分已处理完毕,但前半部分还有剩余的元素,将剩余的元素复制到辅助数组 b[] 中。
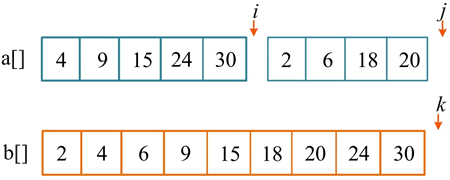
完成合并后,把辅助数组 b[] 中已排好序的元素复制到原数组 a[] 中。
实现代码如下:
递归求解两个规模为 n/2 的子问题,时间复杂度为 2T(n/2)。完成合并的时间复杂度为 O(n)。
总时间复杂度如下:
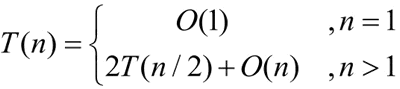
当 n>1 时,递推求解:

递推最终的规模为 1,令 n=2^x,则 x=logn,则:
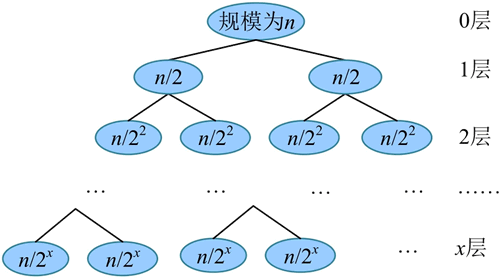
进行递归调用时所使用的栈空间为递归树的深度,递归树如下图所示。递归调用的底层元素数量为 1,因此 n=2x,x=logn,递归树的深度为 logn。空间复杂度为 O(n)。
可以先将待排序元素分解为两个规模大致相等的子序列,若不易解决,则继续分解子序列,直到子序列中的元素数量为 1。因为单个元素的序列本身是有序的,所以此时便可以进行合并,从而得到一个完整的有序序列。
归并排序算法步骤
- 分解:将待排序元素分解为两个规模大致相等的子序列;
- 治理:对两个子序列分别进行归并排序;
- 合并:将两个有序子序列合并为一个有序序列。
归并排序算法完美图解
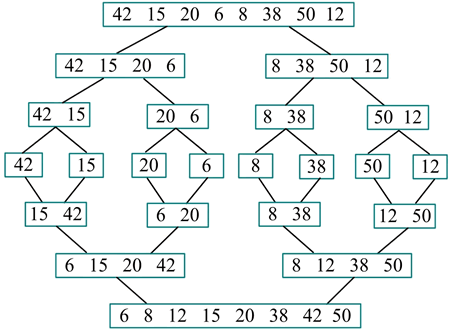
给定一个数列(42,15,20,6,8,38,50,12),执行归并排序的过程如下图所示。
从上图可以看出,首先将待排序元素分解为两个规模大致相等的子序列,然后分别把子序列分解为两个规模大致相等的子序列,如此下去,直到子序列中只剩一个元素时为止,这时含有一个元素的子序列就是有序的。
然后将两个有序子序列合并为一个有序序列,如此下去,直到所有元素都被合并为一个有序序列时为止。
归并排序算法设计
1) 合并操作
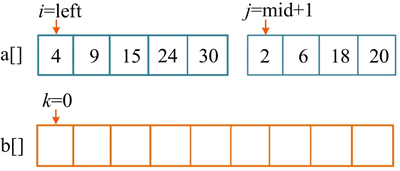
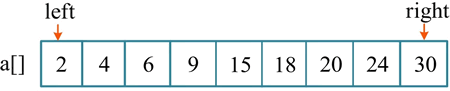
合并操作将两个有序子序列 a[left:mid] 和 a[mid+1:right] 合并为一个有序序列。其中,left、right 表示待合并的两个子序列在数组中的下界和上界,mid 表示下界和上界的中间位置,如下图所示:
为实现合并操作,设置三个变量 i、j、k 和一个辅助数组 b[]:
- i 和 j 分别表示两个待排序子序列中当前待比较元素的位置下标;
- k 表示辅助数组;
- b[] 中待放置元素的位置下标。
比较 a[i] 和 a[j],将较小的赋值给 b[k],同时将相应的变量向后移动。如此下去,直到将所有元素都处理完毕。最后将辅助数组中已排好序的元素复制到原数组 a[] 中,如下图所示。

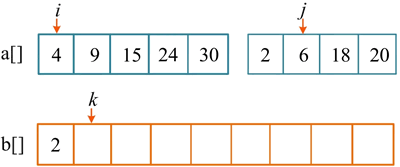
第 1 次比较,a[i]=4,a[j]=2,将较小的元素 2 放入辅助数组 b[],j++,k++。

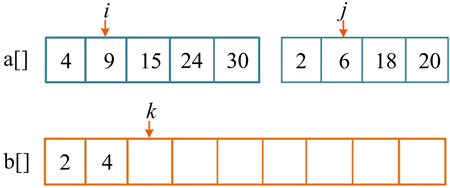
第 2 次比较,a[i]=4,a[j]=6,将较小的元素 4 放入辅助数组 b[],i++,k++。

第 3 次比较,a[i]=9,a[j]=6,将较小的元素 6 放入辅助数组 b[],j++,k++。

第 4 次比较,a[i]=9,a[j]=18,将较小的元素 9 放入辅助数组 b[],i++,k++。

第 5 次比较,a[i]=15,a[j]=18,将较小的元素 15 放入辅助数组 b[],i++,k++。

第 6 次比较,a[i]=24,a[j]=18,将较小的元素 18 放入辅助数组 b[],j++,k++。

第 7 次比较,a[i]=24,a[j]=20,将较小的元素 20 放入辅助数组 b[],j++,k++。

此时,j>right,后半部分已处理完毕,但前半部分还有剩余的元素,将剩余的元素复制到辅助数组 b[] 中。

完成合并后,把辅助数组 b[] 中已排好序的元素复制到原数组 a[] 中。

实现代码如下:
void merge(int left, int mid, int right) { // 合并
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) { // 按从小到大的顺序复制到辅助数组 b[] 中
if (a[i] <= a[j])
b[k++] = a[i++];
else
b[k++] = a[j++];
}
while (i <= mid) b[k++] = a[i++]; // 将数组中剩余的元素复制到辅助数组 b[] 中
while (j <= right) b[k++] = a[j++];
for (i = left, k = 0; i <= right; i++)
a[i] = b[k++];
}
2) 归并排序的实现
首先将原序列分解成两个子序列,然后对两个子序列分别进行递归排序,最后把两个有序子序列合并成一个有序序列。
void mergesort(int left, int right) {
if (left < right) {
int mid = (left + right) / 2; // 取中点
mergesort(left, mid); // 对 a[left:mid] 中的元素进行归并排序
mergesort(mid + 1, right); // 对 a[mid+1:right] 中的元素进行归并排序
merge(left, mid, right); // 合并
}
}
归并排序算法分析
1) 时间复杂度
分解仅仅是计算出子序列的中间位置,时间复杂度为 O(1)。递归求解两个规模为 n/2 的子问题,时间复杂度为 2T(n/2)。完成合并的时间复杂度为 O(n)。
总时间复杂度如下:
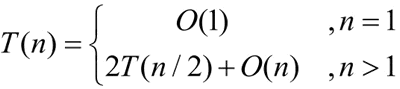
当 n>1 时,递推求解:

递推最终的规模为 1,令 n=2^x,则 x=logn,则:
T(n)=nT(1)+log nO(n) =n+lognO(n) =O(nlogn)可以看出,归并排序的时间复杂度为 O(nlogn)。
2) 空间复杂度
程序中的变量占用的辅助空间都是常数阶的,但进行合并时需要的辅助数组大小为 n。进行递归调用时所使用的栈空间为递归树的深度,递归树如下图所示。递归调用的底层元素数量为 1,因此 n=2x,x=logn,递归树的深度为 logn。空间复杂度为 O(n)。

 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: