基数排序算法(图文并茂,Java实现)
基数排序主要是利用多个关键字进行排序,在日常生活中,扑克牌就是一种多关键字的排序问题。扑克牌有 4 种花色,即红桃、方块、梅花和黑桃,每种花色从 A 到 K 共 13 张牌。这 4 种花色就相当于 4 个关键字,而每种花色从 A 到 K 就相当于对不同的关键字进行排序。
基数排序正是借助这种思想,对不同类的元素进行分类,然后对同一类元素进行排序,通过这样的过程完成对元素序列的排序。在基数排序中,通常将对不同元素的分类称为分配,排序的过程称为收集。
基数排序具体算法思想是,假设第 i 个元素 ai 的关键字为 keyi,keyi 是由 d 位十进制数组成的,即 keyi=kidkid-1…ki1,其中 ki1 为最低位,kid 为最高位。关键字的每一位数字都可作为一个子关键字。首先将元素序列按照最低的关键字进行排序,然后从低位到高位直到最高位依次进行排序,这样就完成了排序过程。
例如,一组元素序列的关键字为 (334,45,21,467,821,562,342,45)。这组关键字最多为 3 位,在排序之前,首先将所有的关键字都看作一个由 3 位数字组成的数,即(324,285,021,467,821,562,342,045)。
对这组关键字进行基数排序需要进行 3 趟分配和收集:
一般情况下,可采用链表实现基数排序。对最低位进行分配和收集的过程如下图所示。其中,数组 f[i] 保存第 i 个链表的头指针,数组 r[i] 保存第 i 个链表的尾指针。
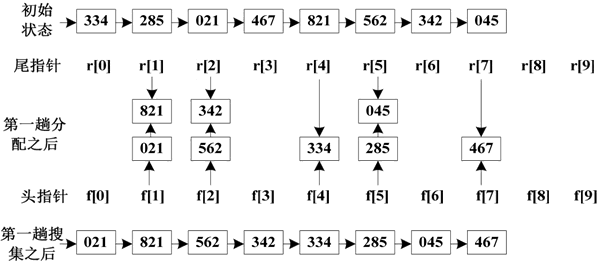
图 1 第一趟分配和收集的过程
对十位数字分配和收集的过程如下图所示:
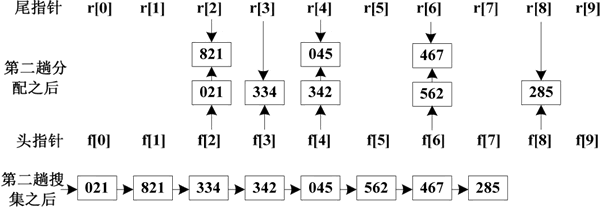
图 2 第二趟分配和收集的过程
对百位数字分配和收集的过程如下图所示:
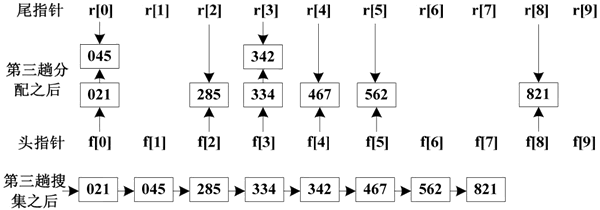
图 3 第三趟分配和收集的过程
经过第一趟排序,即将个位数字作为关键字进行分配后,关键字被分为 10 类,个位数字相同的数字被划分为一类,然后对分配后的关键字进行收集,得到以个位数字非递减排序的序列。
同理,经过第二趟分配和收集后,得到以十位数字非递减排序的序列。经过第三趟分配和收集后,得到最终的排序结果。
基数排序的算法主要包括分配和收集。链表类型描述如下:
基数排序的分配算法实现如下:
其中,数组 f[j] 和 r[j] 分别存放第 j 个子表的第一个元素的位置和最后一个元素的位置。基数排序的收集算法实现如下:
基数排序通过多次调用分配算法和收集算法来实现排序,其算法实现如下:
容易看出,基数排序需要 2radix 个队列指针,分别指向每个队列的队头和队尾。假设待排序的元素为 n 个,每个元素的关键字为 d 个,则基数排序的时间复杂度为 O(d×(n+radix))。
基数排序正是借助这种思想,对不同类的元素进行分类,然后对同一类元素进行排序,通过这样的过程完成对元素序列的排序。在基数排序中,通常将对不同元素的分类称为分配,排序的过程称为收集。
基数排序具体算法思想是,假设第 i 个元素 ai 的关键字为 keyi,keyi 是由 d 位十进制数组成的,即 keyi=kidkid-1…ki1,其中 ki1 为最低位,kid 为最高位。关键字的每一位数字都可作为一个子关键字。首先将元素序列按照最低的关键字进行排序,然后从低位到高位直到最高位依次进行排序,这样就完成了排序过程。
例如,一组元素序列的关键字为 (334,45,21,467,821,562,342,45)。这组关键字最多为 3 位,在排序之前,首先将所有的关键字都看作一个由 3 位数字组成的数,即(324,285,021,467,821,562,342,045)。
对这组关键字进行基数排序需要进行 3 趟分配和收集:
- 首先需要对该关键字序列的最低位进行分配和搜集;
- 然后对十位数字进行分配和收集;
- 最后对最高位数字进行分配和收集。
一般情况下,可采用链表实现基数排序。对最低位进行分配和收集的过程如下图所示。其中,数组 f[i] 保存第 i 个链表的头指针,数组 r[i] 保存第 i 个链表的尾指针。

图 1 第一趟分配和收集的过程
对十位数字分配和收集的过程如下图所示:

图 2 第二趟分配和收集的过程
对百位数字分配和收集的过程如下图所示:

图 3 第三趟分配和收集的过程
经过第一趟排序,即将个位数字作为关键字进行分配后,关键字被分为 10 类,个位数字相同的数字被划分为一类,然后对分配后的关键字进行收集,得到以个位数字非递减排序的序列。
同理,经过第二趟分配和收集后,得到以十位数字非递减排序的序列。经过第三趟分配和收集后,得到最终的排序结果。
基数排序的算法主要包括分配和收集。链表类型描述如下:
class SListCell // 链表的结点类型
{
String key[]; // 关键字
int next;
final int MaxKeyNum=20;
SListCell(int keynum)
{
key = new String[keynum]; // 关键字
next = -1;
}
SListCell()
{
key = new String[MaxKeyNum]; // 关键字
next = -1;
}
}
public class RadixSort
{
SListCell data[];
int keynum;
int length;
RadixSort(int keynum, int length)
{
this.length = length; // 链表的当前长度
data = new SListCell[length + 1]; // 存储元素,data[0] 为头结点
this.keynum = keynum; // 每个元素的当前关键字个数
for (int i = 0; i <= length; i++) {
data[i] = new SListCell(length + 1);
for (int j = 0; j < keynum; j++) {
data[i].key[j] = new String();
}
}
}
}
基数排序的分配算法实现如下:
public void Distribute(int i, int f[], int r[], int radix)
// 为 data 中的第 i 个关键字 key[i] 建立 radix 个子表,使同一子表中的元素的 key[i] 相同
// f[0···radix - 1] 和 r[0···radix - 1] 分别指向各个子表中第一个元素和最后一个元素
{
for(int j=0; j<radix; j++) // 将各个子表初始化为空表
f[j] = 0;
int p = data[0].next;
while(p != 0) {
int j = Integer.parseInt(data[p].key[i]); // 将对应的关键字字符转换为整数类型
if (f[j] == 0) // 若 f[j] 是空表,则 f[j] 指示第一个元素
f[j] = p;
else
data[r[j]].next = p;
r[j] = p; // 将 p 所指的结点插入第 j 个子表中
p = data[p].next;
}
}
其中,数组 f[j] 和 r[j] 分别存放第 j 个子表的第一个元素的位置和最后一个元素的位置。基数排序的收集算法实现如下:
public void Collect(int f[], int r[], int radix)
// 按 key[i] 将 f[0···Radix - 1] 所指的各个子表依次链接成一个链表
{
int j = 0;
while(f[j] == 0) // 找第一个非空子表
j++;
data[0].next = f[j]; // data[0].next 指向第一个非空子表中的第一个结点
int t = r[j];
while(j<radix - 1) {
j++;
while (j < radix - 1 && f[j] == 0) // 找下一个非空子表
j++;
if (f[j] != 0) // 将非空链表链接在一起
{
data[t].next = f[j];
t = r[j];
}
}
data[t].next = 0; // t 指向最后一个非空子表中的最后一个结点
}
基数排序通过多次调用分配算法和收集算法来实现排序,其算法实现如下:
public void RadixSort(int radix)
// 对 L 进行基数排序,使得 L 成为按关键字非递减的链表,L.r[0] 为头结点
{
int f[] = new int[radix];
int r[] = new int[radix];
for(int j=0; j<radix; j++) // 将各个子表初始化为空表
f[j]=0;
for(int j=0; j<radix; j++) // 将各个子表初始化为空表
r[j]=0;
for(int i=0; i<keynum; i++) // 由低位到高位依次对各关键字进行分配和收集
{
Distribute(i, f, r, radix); // 第 i 趟分配
Collect(f, r, radix); // 第 i 趟收集
System.out.print("第"+(i+1)+"趟收集后:");
PrintList2();
}
}
容易看出,基数排序需要 2radix 个队列指针,分别指向每个队列的队头和队尾。假设待排序的元素为 n 个,每个元素的关键字为 d 个,则基数排序的时间复杂度为 O(d×(n+radix))。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: