Python求水仙花数详解

所谓的“水仙花数”是指一个三位数，其各位数字的立方和等于该数本身，例如，153 是“水仙花数”，因为 153=13+53+33。

问题分析

根据“水仙花数”的定义，判断一个数是否为“水仙花数”最重要的是要把给出的三位数的个位、十位和百位分别拆分，并求其立方和（设为 s），若 s 与给出的三位数相等，则该三位数为“水仙花数”，反之，则不是。

算法设计

“水仙花数”是指满足某一条件的三位数，根据这一信息可以确定整数的取值范围是100～999。对应的循环条件如下：

for n in range(100, 1000)

• 将 n 整除以 100，得出 n 在百位上的数字 hun。
• 将（n-hun×100）整除以 10（或将 n 先整除以 10 再对 10 求模，即 n//10%10），得出 n 在十位上的数字 ten。
• 将 n 对 10 取余，得出 n 在个位上的数字 ind。
• 求得这三个数字的立方和是否与其本身相等，若相等，则该数为“水仙花数”。

对于每个位置上的数值将其拆分的算法有很多种，应根据不同情况选择不同的算法（对于同一问题不同算法的效率有时会相差很多）。

确定程序框架

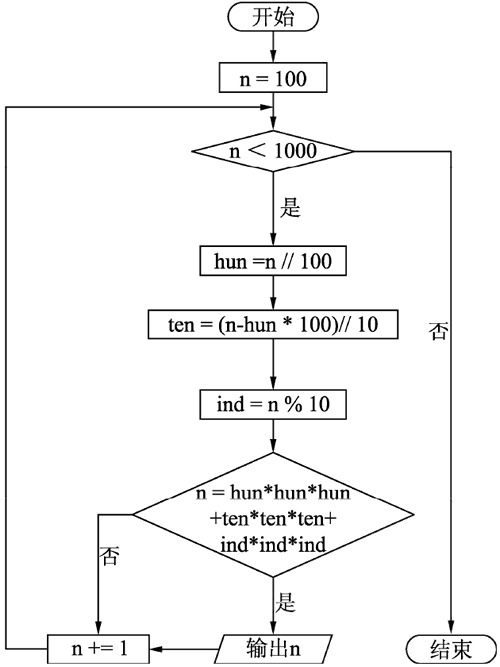
程序流程图如下图所示：

完整的程序

if __name__ == '__main__':
    print("result is: ")
    # 整数的取值范围
    for n in range(100, 1000):
        hun = n // 100 # 百位
        ten = (n - hun * 100) // 10 # 十位
        ind = n % 10 # 个位
        m = hun*hun*hun + ten*ten*ten + ind*ind*ind # 求和
        if n == m: # 各位上的立方和是否与原数n相等
            print("%d \t" %n, end=" ")

程序运行结果为：

result is:
153   370       371       407

求某个数 n 的立方，可以采用程序中的方法对 n 连乘三次 n×n×n，求五次方、十次方运用这种方法仍可忍受，但如果要求的是 n 的 50 次方甚至更大呢？也要像上面一样写 50 次吗？对于编程者来说这是很痛苦的一种事情，既浪费时间又浪费精力。

因此，Python 语言为我们提供了幂运算符“**”，例如求 5 的 3 次方，可以表示为 5**3，故我们可以换一种写法，程序代码如下：

if __name__ == '__main__':
    print("result is: ")
    for n in range(100, 1000): # 整数的取值范围
        hun = n // 100 # 百位
        ten = (n - hun * 100) // 10 # 十位
        ind = n % 10 # 个位
        m = hun**3 + ten**3 + ind**3
        if n == m: # 各位上的立方和是否与原数n相等
            print("%d \t" %n, end=" ")

程序运行结果为：

result is:
153   370       371       407