C++递归函数详解(图文并茂,附带实例)
递归调用是函数内部调用自身的过程。递归必须要有结束条件,否则会进入无限递归状态,永远无法结束。
例如求 n!(n!=1×2×3×…×n),因为 n! = n × (n-1)!,所以可以进行递归调用,只对特殊情况进行判断,将其作为递归结束条件。当 n=0 或者 n=1 时直接返回 1,在其他情况下直接进行递归调用。
阶乘是典型的递归调用方式,5 的阶乘递推、回归过程如下图所示:
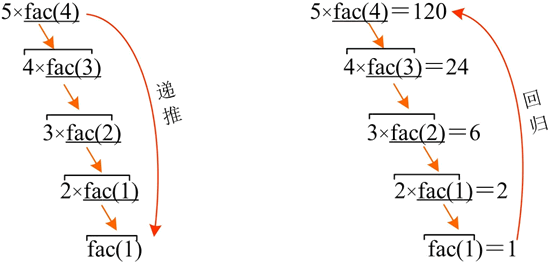
上图中的递推、回归过程是从逻辑思维上推理并用图进行形象表达的,但其在计算机内部是被怎样处理的呢?计算机使用了一种被称为“栈”的数据结构,它类似于一个放了一摞盘子的容器,每次放进去一个,拿出来的时候只能从顶端拿一个,不允许从中间插入或抽取,因此被称为“后进先出”(Last In First Out,LIFO)。
5 的阶乘递推(入栈)过程的形象表达如下图所示,在实际递归中传递的是参数的地址:
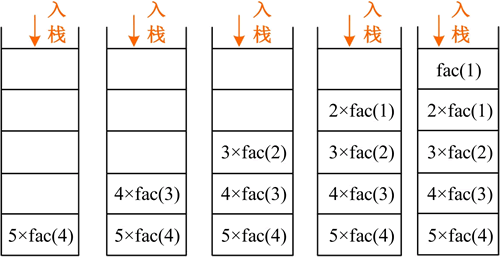
5 的阶乘回归(出栈)过程的形象表达如下图所示,首先一步步地让子问题入栈,直到直接可解,得到返回值,再一步步地出栈,最终得到递归结果。在运算过程中使用了 5 个栈空间作为辅助空间。
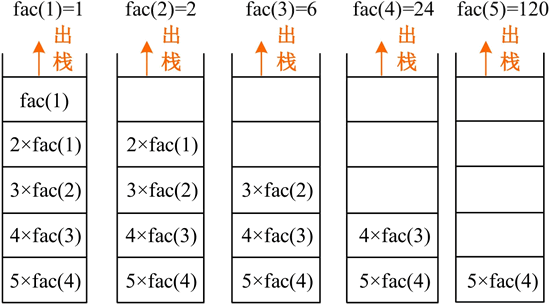
【实例 1】斐波那契数列的第 1 个数和第 2 个数都为 1,接下来的每个数都等于前面两个数之和。给出一个正整数 k,请输出斐波那契数列中的第 k 个数。
解析:斐波那契数列的递归表达式如下:
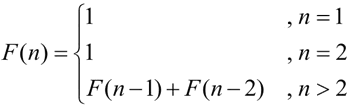
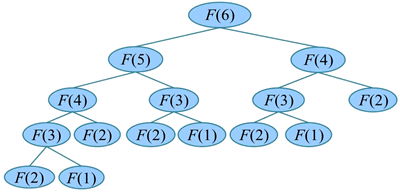
以 F(6) 为例,递归求解过程如下图所示:
代码如下:
【实例 2】小鱼最近参加了一个数字游戏,需要把看到的一串数字记住后反着念出来。这对小鱼来说实在是太难了,请你帮小鱼解决这个问题。输入一串以空格隔开的整数,以 0 结束。
解析:本题要求逆序输出一个序列,这既可以通过栈实现,也可以通过递归算法实现。
【实例 3】:输入两个整数 a 和 b,求它们的最大公约数(gcd)和最小公倍数(lcm)。这两个整数均为 int 类型。
解析:本题求解最大公约数和最小公倍数。对于最大公约数,可以通过辗转相除法求解,当 m=0 时,直接返回 n,否则递归求解 m 和 n%m 的最大公约数。两个数的最小公倍数等于两数之积除以两数的最大公约数。
例如求 n!(n!=1×2×3×…×n),因为 n! = n × (n-1)!,所以可以进行递归调用,只对特殊情况进行判断,将其作为递归结束条件。当 n=0 或者 n=1 时直接返回 1,在其他情况下直接进行递归调用。
#include <iostream>
using namespace std;
int fac(int n) {
if (n == 0 || n == 1) return 1;
return n * fac(n - 1);
}
int main() {
int n;
cin >> n;
cout << fac(n);
return 0;
}
运行结果为:
4
24
递归的原理
递归包括递推和回归:- 递推指先将原问题不断分解为子问题,直到达到结束条件,返回最近子问题的解;
- 然后逆向逐一回归,最终到达递推开始时的原问题,返回原问题的解。
阶乘是典型的递归调用方式,5 的阶乘递推、回归过程如下图所示:

上图中的递推、回归过程是从逻辑思维上推理并用图进行形象表达的,但其在计算机内部是被怎样处理的呢?计算机使用了一种被称为“栈”的数据结构,它类似于一个放了一摞盘子的容器,每次放进去一个,拿出来的时候只能从顶端拿一个,不允许从中间插入或抽取,因此被称为“后进先出”(Last In First Out,LIFO)。
5 的阶乘递推(入栈)过程的形象表达如下图所示,在实际递归中传递的是参数的地址:

5 的阶乘回归(出栈)过程的形象表达如下图所示,首先一步步地让子问题入栈,直到直接可解,得到返回值,再一步步地出栈,最终得到递归结果。在运算过程中使用了 5 个栈空间作为辅助空间。

【实例 1】斐波那契数列的第 1 个数和第 2 个数都为 1,接下来的每个数都等于前面两个数之和。给出一个正整数 k,请输出斐波那契数列中的第 k 个数。
解析:斐波那契数列的递归表达式如下:
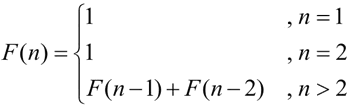
以 F(6) 为例,递归求解过程如下图所示:

代码如下:
#include <iostream>
using namespace std;
int fib(int n) {
if (n == 1 || n == 2) // 进行特殊情况判断,直接返回结果
return 1;
return fib(n - 1) + fib(n - 2); // 递归调用,当前项等于前两项之和
}
int main() {
int n, k;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> k;
cout << fib(k) << endl;
}
return 0;
}
运行结果为:
3
6
8
4
3
3
2
【实例 2】小鱼最近参加了一个数字游戏,需要把看到的一串数字记住后反着念出来。这对小鱼来说实在是太难了,请你帮小鱼解决这个问题。输入一串以空格隔开的整数,以 0 结束。
解析:本题要求逆序输出一个序列,这既可以通过栈实现,也可以通过递归算法实现。
#include <iostream>
using namespace std;
void print(int x) {
cin >> x;
if (x == 0) return; // 递归结束条件
print(x); // 递归调用
cout << x << " "; // 调用结束时输出 x
}
int main() {
print(5); // 示例调用,可以根据需要修改
return 0;
}
运行结果为:
1
2
3
4
0
4 3 2 1
【实例 3】:输入两个整数 a 和 b,求它们的最大公约数(gcd)和最小公倍数(lcm)。这两个整数均为 int 类型。
解析:本题求解最大公约数和最小公倍数。对于最大公约数,可以通过辗转相除法求解,当 m=0 时,直接返回 n,否则递归求解 m 和 n%m 的最大公约数。两个数的最小公倍数等于两数之积除以两数的最大公约数。
#include <iostream>
using namespace std;
int gcd(int n, int m) { // 最大公约数
if (m == 0) return n;
return gcd(m, n % m);
}
long long lcm(int n, int m) { // 最小公倍数,定义为 long long 类型,以免溢出
return (long long)n * m / gcd(n, m); // 需要转换为 long long 类型,以免溢出
}
int main() {
int a, b;
cin >> a >> b;
cout << gcd(a, b) << " " << lcm(a, b); // 输出 a 和 b 的最大公约数、最小公倍数
return 0;
}
运行结果为:
8 9
1 72
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: