Dijkstra迪杰斯特拉算法详解(Java实现)
在日常生活中,经常会遇到求两个地点之间的最短距离的问题,如在交通网络中求城市 A 与城市 B 的最短路径。可以将每个城市作为图的顶点,两个城市的线路作为图的弧或者边,城市之间的距离作为权值,这样就把一个实际的问题转换为求图的顶点之间的最短路径问题。
求图的最短路径的算法有两种,分别是 Dijkstra(迪杰斯特拉)算法和 Floyd(弗洛伊德)算法:
本节重点介绍 Dijkstra 算法。
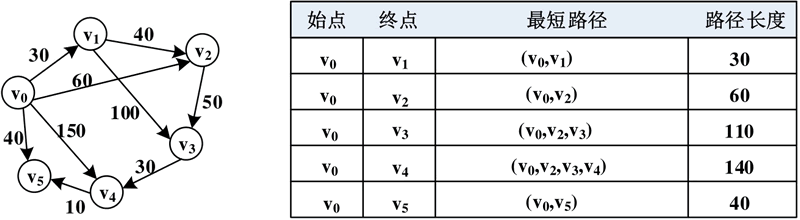
图 1 带权有向图及从顶点v0到其他各个顶点的最短路径
从图 1 中可以看出,从顶点 v0 到顶点 v2 有两条路径 (v0,v1,v2) 和 (v0,v2),其中前者的路径长度为 70,后者的路径长度为 60。因此,(v0,v2) 是从顶点 v0 到顶点 v2 的最短路径。
从顶点 v0 到顶点 v3 有 3 条路径,分别是 (v0,v1,v2,v3)、(v0,v2,v3) 和 (v0,v1,v3)。其中,第 1 条路径长度为 120,第 2 条路径长度为 110,第 3 条路径长度为 130。因此,(v0,v2,v3) 是从顶点 v0 到顶点 v3 的最短路径。
下面介绍由 Dijkstra 提出的求最短路径的算法。它的基本思想是根据路径长度递增求解从顶点 v0 到其他各顶点的最短路径。
设有一个带权有向图 D=(V,E),定义一个数组 dist,数组中的每个元素 dist[i]表示顶点 v0 到顶点 vi 的最短路径长度,则长度为 dist[j]=Min{dist[i]|vi∈V} 的路径,表示从顶点 v0 出发到顶点 vj 的最短路径。
也就是说,在所有的顶点 v0 到顶点 vi 的路径中,dist[j] 是最短的一条路径。而数组 dist 的初始状态是:若从顶点 v0 到顶点 vj 存在弧,则 dist[j] 的值是弧 <v0,vj>的权值,否则 dist[j] 的值为 ∞。
假设 S 表示求出的最短路径对应终点的集合。在按递增次序求出从顶点 v0 出发到顶点 vj 的最短路径之后,下一条最短路径是从顶点 v0 到顶点 vk 的最短路径,要么是弧 <v0,vk>,要么是经过集合 S 中某个顶点后到达顶点 vk 的路径。从顶点 v0 出发到顶点 vk 的最短路径的长度要么是弧 <v0,vk> 的权值,要么是 dist[j] 与 vj 到 vk 的权值之和。
求最短路径的长度满足:终点为 vx 的最短路径要么是弧 <v0,vx>,要么是中间经过集合 S 中某个顶点后到达顶点 vx 所经过的路径。
例如,从图 1 可以看出,(v0,v2) 是从 v0 到 v2 的最短路径,(v0,v2,v3) 是从 v0 到 v3 的最短路径,经过了顶点 v2;(v0,v2,v3,v4) 是从 v0 到 v4 的最短路径,经过了顶点 v3。
在一般情况下,下一条最短路径的长度一定是:
Dijkstra 算法求解最短路径的步骤如下(假设有向图用邻接矩阵存储):
利用 Dijkstra 算法求最短路径的思想,对如图 1 所示的有向图求解从顶点 v0 到其他顶点的最短路径,求解过程如下图所示。
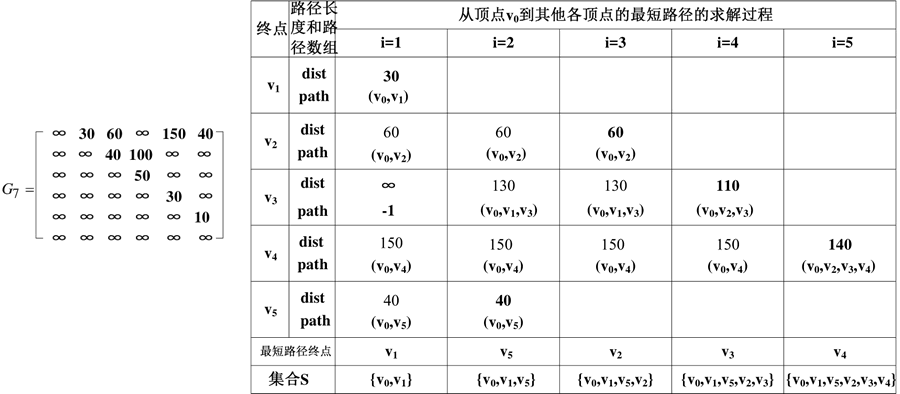
图 2 带权图从顶点 v0 到其他各顶点的最短路径的求解过程
根据 Dijkstra 算法,求带权图的最短路径的过程中,数组 dist[] 和 path[] 的变化情况如下图所示。

图 3 求最短路径各变量的状态变化过程
1) 初始化:S={v0}、V-S={v1,v2,v3,v4,v5}、dist[]=[0,30,60,∞,150,40](根据邻接矩阵得到 v0 到其他各顶点的权值)、path[]=[0,0,0,-1,0,0](若顶点 v0 到顶点 vi 有边 <v0,vi> 存在,则它是从 v0 到 vi 的当前最短路径,令 path[i]=0,表示该最短路径上顶点 vi 的前一个顶点是 v0;若 v0 到 vi 没有路径,则令 path[i]=-1)。
2) 从 V-S 集合中找到一个顶点,该顶点与 S 集合中的顶点构成的路径最短,即 dist[] 数组中值最小的顶点为 v1,将其添加到 S 中,则 S={v0,v1}、V-S={v2,v3,v4,v5}。考察顶点 v1,发现从 v1 到 v2 和 v3 存在边,则得到:
3) 从 V-S 中找到一个顶点 v5,它与 S 中顶点构成的路径最短,即 dist[] 数组中值最小的顶点,将其添加到 S 中,则 S={v0,v1,v5}、V-S={v2,v3,v4}。考察顶点 v5,发现 v5 与其他顶点不存在边,则 dist[] 和 path[] 保持不变。
4) 从 V-S 中找到一个顶点 v2,它与 S 中顶点构成的路径最短,即 dist[] 数组中值最小的顶点,将其加入 S 中,则 S={v0,v1,v5,v2}、V-S={v3,v4}。考察顶点 v2,从 v2 到 v3 存在边,得到:
5) 从 V-S 中找到一个顶点 v3,它与 S 中顶点构成的路径最短,即 dist[] 数组中值最小的顶点,将其加入 S 中,则 S={v0,v1,v5,v2,v3}、V-S={v4}。考察顶点 v3,从 v3 到 v4 存在边,得到:
6) 从 V-S 中找到与 S 中顶点构成的路径最短的顶点 v4,即 dist[] 数组中值最小的顶点,将其加入 S 中,则 S={v0,v1,v5,v2,v3,v4}、V-S={ }。考察顶点 v4,从 v4 到 v5 存在边,得到:
根据 dist[] 和 path[] 中的值输出从 v0 到其他各顶点的最短路径。例如,从 v0 到 v4 的最短路径可根据 path[] 获得:由 path[4]=3 得到 v4 的前驱顶点为 v3,由 path[3]=2 得到 v3 的前驱顶点为 v2,由 path[2]=0 得到 v2 的前驱顶点为 v0,因此反推出从 v0 到 v4 的最短路径为 v0→v2→v3→v4,最短路径长度为 dist[4],即 140。
重复执行以上步骤,直到求出从 v0 到所有其他顶点的最短路径为止。数组 path[v] 存放顶点v的前驱顶点的下标,根据 path[] 中的值,可依次求出相应顶点的前驱,直到源点 v0,逆推回去可得到从 v0 到其他各顶点的最短路径。
该算法的时间主要耗费在第 2 个 for 循环语句,外层 for 循环语句主要控制循环的次数,一次循环可得到从 v0 到某个顶点的最短路径,两个内层 for 循环共执行 n 次,如果不考虑每次求解最短路径的耗费,那么该算法的时间复杂度是 O(n2)。
下面通过一个具体例子来说明 Dijkstra 算法的应用。
【实例】建立一个如图 1 所示的有向网 N,输出有向网 N 中从 v0 出发到其他各顶点的最短路径及从 v0 到各个顶点的最短路径长度。
求图的最短路径的算法有两种,分别是 Dijkstra(迪杰斯特拉)算法和 Floyd(弗洛伊德)算法:
- Dijkstra 算法求解的是图中某一顶点到其余各顶点的最短路径问题,即单源最短路径问题;
- Floyd 算法求解的是图中任何一对顶点的最短路径问题,即多源最短路径问题。
本节重点介绍 Dijkstra 算法。
Dijkstra算法思路
带权有向图及从顶点 v0 出发到其他各个顶点的最短路径如下图所示。
图 1 带权有向图及从顶点v0到其他各个顶点的最短路径
从图 1 中可以看出,从顶点 v0 到顶点 v2 有两条路径 (v0,v1,v2) 和 (v0,v2),其中前者的路径长度为 70,后者的路径长度为 60。因此,(v0,v2) 是从顶点 v0 到顶点 v2 的最短路径。
从顶点 v0 到顶点 v3 有 3 条路径,分别是 (v0,v1,v2,v3)、(v0,v2,v3) 和 (v0,v1,v3)。其中,第 1 条路径长度为 120,第 2 条路径长度为 110,第 3 条路径长度为 130。因此,(v0,v2,v3) 是从顶点 v0 到顶点 v3 的最短路径。
下面介绍由 Dijkstra 提出的求最短路径的算法。它的基本思想是根据路径长度递增求解从顶点 v0 到其他各顶点的最短路径。
设有一个带权有向图 D=(V,E),定义一个数组 dist,数组中的每个元素 dist[i]表示顶点 v0 到顶点 vi 的最短路径长度,则长度为 dist[j]=Min{dist[i]|vi∈V} 的路径,表示从顶点 v0 出发到顶点 vj 的最短路径。
也就是说,在所有的顶点 v0 到顶点 vi 的路径中,dist[j] 是最短的一条路径。而数组 dist 的初始状态是:若从顶点 v0 到顶点 vj 存在弧,则 dist[j] 的值是弧 <v0,vj>的权值,否则 dist[j] 的值为 ∞。
假设 S 表示求出的最短路径对应终点的集合。在按递增次序求出从顶点 v0 出发到顶点 vj 的最短路径之后,下一条最短路径是从顶点 v0 到顶点 vk 的最短路径,要么是弧 <v0,vk>,要么是经过集合 S 中某个顶点后到达顶点 vk 的路径。从顶点 v0 出发到顶点 vk 的最短路径的长度要么是弧 <v0,vk> 的权值,要么是 dist[j] 与 vj 到 vk 的权值之和。
求最短路径的长度满足:终点为 vx 的最短路径要么是弧 <v0,vx>,要么是中间经过集合 S 中某个顶点后到达顶点 vx 所经过的路径。
例如,从图 1 可以看出,(v0,v2) 是从 v0 到 v2 的最短路径,(v0,v2,v3) 是从 v0 到 v3 的最短路径,经过了顶点 v2;(v0,v2,v3,v4) 是从 v0 到 v4 的最短路径,经过了顶点 v3。
在一般情况下,下一条最短路径的长度一定是:
dist[j]=Min{dist[i]|vi∈V-S}
其中,dist[i] 要么是弧 <v0,vi> 的权值,要么是 dist[k](vk∈S) 与弧 <vk,vi> 的权值之和。V-S 表示还没有求出的最短路径的终点集合。Dijkstra 算法求解最短路径的步骤如下(假设有向图用邻接矩阵存储):
- 初始时,S 只包括源点 v0,即 S={v0},V-S 包括除 v0 外的图中的其他顶点。v0 到其他顶点的路径初始化为 dist[i]=G.arc[0][i].adj。
- 选择距离顶点 vi 最短的顶点 vk,使得 dist[k]=Min{dist[i]|vi∈V-S},dist[k]表示从 v0 到 vk 的最短路径长度,vk 表示对应的终点,将 vk 加入 S 中。
- 修改从 v0 到顶点 vi 的最短路径长度,其中 vi∈V-S。若有 dist[k]+G.arc[k][i]<dist[i],则修改 dist[i],使得 dist[i]=dist[k]+G.arc[k][i].adj。
- 重复执行步骤 2 和步骤 3,直到求出所有从 v0 到其他顶点的最短路径长度。
利用 Dijkstra 算法求最短路径的思想,对如图 1 所示的有向图求解从顶点 v0 到其他顶点的最短路径,求解过程如下图所示。

图 2 带权图从顶点 v0 到其他各顶点的最短路径的求解过程
根据 Dijkstra 算法,求带权图的最短路径的过程中,数组 dist[] 和 path[] 的变化情况如下图所示。

图 3 求最短路径各变量的状态变化过程
1) 初始化:S={v0}、V-S={v1,v2,v3,v4,v5}、dist[]=[0,30,60,∞,150,40](根据邻接矩阵得到 v0 到其他各顶点的权值)、path[]=[0,0,0,-1,0,0](若顶点 v0 到顶点 vi 有边 <v0,vi> 存在,则它是从 v0 到 vi 的当前最短路径,令 path[i]=0,表示该最短路径上顶点 vi 的前一个顶点是 v0;若 v0 到 vi 没有路径,则令 path[i]=-1)。
2) 从 V-S 集合中找到一个顶点,该顶点与 S 集合中的顶点构成的路径最短,即 dist[] 数组中值最小的顶点为 v1,将其添加到 S 中,则 S={v0,v1}、V-S={v2,v3,v4,v5}。考察顶点 v1,发现从 v1 到 v2 和 v3 存在边,则得到:
dist[2]=min{dist[2],dist[1]+40}=60
dist[3]=min{dist[3],dist[1]+100}=130(修改)
则 dist[]=[0,30,60,130,150,40],同时,修改 v1 到 v3 路径上的前驱顶点,path[]=[0,0,0,1,0,0]。3) 从 V-S 中找到一个顶点 v5,它与 S 中顶点构成的路径最短,即 dist[] 数组中值最小的顶点,将其添加到 S 中,则 S={v0,v1,v5}、V-S={v2,v3,v4}。考察顶点 v5,发现 v5 与其他顶点不存在边,则 dist[] 和 path[] 保持不变。
4) 从 V-S 中找到一个顶点 v2,它与 S 中顶点构成的路径最短,即 dist[] 数组中值最小的顶点,将其加入 S 中,则 S={v0,v1,v5,v2}、V-S={v3,v4}。考察顶点 v2,从 v2 到 v3 存在边,得到:
dist[3]=min{dist[3],dist[2]+50}=110(修改)
则 dist[]=[0,30,60,110,150,40],同时修改 v1 到 v3 路径上的前驱顶点,path[]=[0,0,0,2,0,0]。5) 从 V-S 中找到一个顶点 v3,它与 S 中顶点构成的路径最短,即 dist[] 数组中值最小的顶点,将其加入 S 中,则 S={v0,v1,v5,v2,v3}、V-S={v4}。考察顶点 v3,从 v3 到 v4 存在边,得到:
dist[4]=min{dist[4],dist[3]+30}=140(修改)
则 dist[]=[0,30,60,110,140,40],同时修改 v1 到 v4 路径上的前驱顶点,path[]=[0,0,0,2,3,0]。6) 从 V-S 中找到与 S 中顶点构成的路径最短的顶点 v4,即 dist[] 数组中值最小的顶点,将其加入 S 中,则 S={v0,v1,v5,v2,v3,v4}、V-S={ }。考察顶点 v4,从 v4 到 v5 存在边,得到:
dist[5]=min{dist[5],dist[4]+10}=40
则 dist[] 和 path[] 保持不变,即 dist[]=[0,30,60,110,140,40]、path[]=[0,0,0,2,3,0]。根据 dist[] 和 path[] 中的值输出从 v0 到其他各顶点的最短路径。例如,从 v0 到 v4 的最短路径可根据 path[] 获得:由 path[4]=3 得到 v4 的前驱顶点为 v3,由 path[3]=2 得到 v3 的前驱顶点为 v2,由 path[2]=0 得到 v2 的前驱顶点为 v0,因此反推出从 v0 到 v4 的最短路径为 v0→v2→v3→v4,最短路径长度为 dist[4],即 140。
Dijkstra算法实现
求解最短路径的 Dijkstra 算法描述如下:
public void Dijkstra(MGraph M, int v0, int path[], double dist[], int set[])
// 用 Dijkstra 算法求有向网 N 的 v0 顶点到其余各顶点 v 的最短路径 path[v] 及带权长度 dist[v]
// final[v] 为 1 表示 v∈S,即已经求出从 v0 到 v 的最短路径
{
int k = 0;
for (int v = 0; v < M.vexnum; v++) // 数组 dist 存储 v0 到 v 的最短距离,初始化为 v0 到 v 的弧的距离
{
set[v] = 0;
dist[v] = M.arc[v0][v]; // 记录与 v0 有连接的顶点的权值
if (M.arc[v0][v] < Double.POSITIVE_INFINITY)
path[k++] = v0;
else
path[k++] = -1; // 初始化路径数组 path 为 -1
}
dist[v0] = 0; // v0 到 v0 的路径为 0
set[v0] = 1; // v0 顶点并入集合 S
path[v0] = v0;
// 从 v0 到其余 G.vexnum-1 个顶点的最短路径,并将该顶点并入集合 S
// 利用循环每次求 v0 到某个顶点 v 的最短路径
for (int v = 1; v < M.vexnum; v++) {
double min = Double.POSITIVE_INFINITY; // 记录一次循环距离 v0 最近的距离
for (int w = 0; w < M.vexnum; w++) // 找出距 v0 最近的顶点
// final[w] 为 0 表示该顶点还没有记录与它最近的顶点
{
if (set[w] == 0 && dist[w] < min) // 在不属于集合 S 的顶点中找到离 v0 最近的顶点
{
k = w;
min = dist[w]; // 记录最小权值
}
}
// 将目前找到的最接近 v0 的顶点的下标的位置置为 1,表示该顶点已被记录
set[k] = 1;
// 修正当前最短路径,即距离
for (int w = 0; w < M.vexnum; w++) // 利用新并入集合 S 的顶点,更新 v0 到不属于 S 的顶点的最短路径长度和最短路径数组
// 若经过顶点 v 的路径比现在这条路径短,则修改顶点 v0 到 w 的距离
{
if (set[w] == 0 && min < Double.POSITIVE_INFINITY && M.arc[k][w] < Double.POSITIVE_INFINITY && min + M.arc[k][w] < dist[w])
{
dist[w] = min + M.arc[k][w]; // 修改顶点 w 距离 v0 的最短长度
path[w] = k; // 存储最短路径前驱结点的下标
}
}
}
}
public void PrintShortPath(MGraph M, int v0, int path[], double dist[]) {
int k = 0;
int[] apath = new int[M.vexnum];
System.out.println("存储最短路径前驱结点下标的数组 path 的值为:");
System.out.print("数组下标:");
for (int i = 0; i < M.vexnum; i++)
System.out.print(i + " ");
System.out.print("\n数组的值:");
for (int i = 0; i < M.vexnum; i++) {
System.out.print(path[i] + " ");
}
// 存储最短路径前驱结点下标的数组 path 的值为:
// 数组下标:0 1 2 3 4 5
// 数组的值:0 0 0 2 3 0
// 当 path[4]=3 时表示,顶点 4 的前驱结点是顶点 3
// 找到顶点 3,有 path[3]=2,表示顶点 3 的前驱结点是顶点 2
// 找到顶点 2,有 path[2]=0,表示顶点 2 的前驱结点是顶点 0
// 因此由顶点 4 到顶点 0 的最短路径为:4 -> 3 -> 2 -> 0
// 将这个顺序倒过来即可得到顶点 0 到顶点 4 的最短路径
System.out.println("\nv0 到其他顶点的最短路径如下:");
for (int i = 1; i < M.vexnum; i++) {
k = 0;
System.out.print("v" + v0 + " -> v" + i + ": ");
int j = i;
System.out.print(M.vex[v0] + " ");
while (path[j] != 0) {
apath[k] = path[j];
j = path[j];
k += 1;
}
for (j = k - 1; j > -1; j--)
System.out.print(M.vex[apath[j]] + " ");
System.out.println(M.vex[i]);
}
System.out.println("顶点 v" + v0 + " 到各顶点的最短路径长度为:");
for (int i = 1; i < M.vexnum; i++)
System.out.println(M.vex[0] + " - " + M.vex[i] + ": " + dist[i]); // dist 数组中存放 v0 到各顶点的最短路径
}
其中,数组 dist[v] 表示从顶点 v0 到顶点 v 当前求出的最短路径长度。先利用 v0 到其他顶点的弧对应的权值初始化数组 path[] 和 dist[],然后找出从 v0 到顶点 v(不属于集合 S)的最短路径,并将 v 并入集合 S,最短路径长度赋给 min。接着利用新并入的顶点 v,更新 v0 到其他顶点(不属于集合 S)的最短路径长度和直接前驱顶点。重复执行以上步骤,直到求出从 v0 到所有其他顶点的最短路径为止。数组 path[v] 存放顶点v的前驱顶点的下标,根据 path[] 中的值,可依次求出相应顶点的前驱,直到源点 v0,逆推回去可得到从 v0 到其他各顶点的最短路径。
该算法的时间主要耗费在第 2 个 for 循环语句,外层 for 循环语句主要控制循环的次数,一次循环可得到从 v0 到某个顶点的最短路径,两个内层 for 循环共执行 n 次,如果不考虑每次求解最短路径的耗费,那么该算法的时间复杂度是 O(n2)。
下面通过一个具体例子来说明 Dijkstra 算法的应用。
【实例】建立一个如图 1 所示的有向网 N,输出有向网 N 中从 v0 出发到其他各顶点的最短路径及从 v0 到各个顶点的最短路径长度。
public static void main(String args[]) {
int vnum = 6;
int arcnum = 9;
class Weight {
int v1, v2;
double w;
}
double w[][] = {{0, 1, 30}, {0, 2, 60}, {0, 4, 150}, {0, 5, 40}, {1, 2, 40}, {1, 3, 100}, {2, 3, 50}, {3, 4, 30}, {4, 5, 10}};
String ch[] = {"v0", "v1", "v2", "v3", "v4", "v5"};
int path[] = new int[vnum]; // 存放最短路径所经过的顶点
double dist[] = new double[vnum]; // 存放最短路径长度
MGraph N = new MGraph();
int[] set = new int[vnum];
N.CreateGraph(w, vnum, arcnum, ch); // 创建有向网 N
N.DisplayGraph(); // 输出有向网 N
ShortestPath ShortPath = new ShortestPath();
ShortPath.Dijkstra(N, 0, path, dist, set);
ShortPath.PrintShortPath(N, 0, path, dist); // 打印最短路径
}
程序运行结果如下:
有向网具有 6 个顶点 9 条弧,顶点依次是:v0 v1 v2 v3 v4 v5
有向网 N 的:
序号 i=
0 1 2 3 4 5
0 ∞ 30 60 ∞ 150 40
1 ∞ ∞ 40 100 ∞ ∞
2 ∞ ∞ ∞ 50 ∞ ∞
3 ∞ ∞ ∞ ∞ 30 ∞
4 ∞ ∞ ∞ ∞ ∞ 10
5 ∞ ∞ ∞ ∞ ∞ ∞
存储最短路径前驱结点下标的数组 path 的值为:
数组下标:0 1 2 3 4 5
数组的值:0 0 0 2 3 0
v0 到其他顶点的最短路径如下:
v0 -> v1: v0 v1
v0 -> v2: v0 v2
v0 -> v3: v0 v2 v3
v0 -> v4: v0 v2 v3 v4
v0 -> v5: v0 v5
顶点 v0 到各顶点的最短路径长度为:
v0 -> v1: 30.0
v0 -> v2: 60.0
v0 -> v3: 110.0
v0 -> v4: 140.0
v0 -> v5: 40.0
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: