平衡二叉树详解(Java实现)
二叉排序树查找在最坏的情况下,二叉排序树的深度为 n,其平均查找长度为 n。为了减小二叉排序树的查找次数,需要进行平衡化处理,平衡化处理得到的二叉树称为平衡二叉树。
若将二叉树中结点的平衡因子定义为结点的左子树与右子树之差,则平衡二叉树中每个结点的平衡因子的值只有 3 种可能:-1、0 和 1。
例如,如下图所示为平衡二叉树:
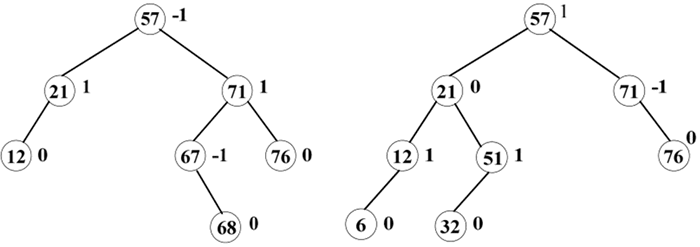
图 1 平衡二叉树
结点的右边表示平衡因子,因为该二叉树既是二叉排序树又是平衡树,因此该二叉树称为平衡二叉排序树。
若在二叉树中有一个结点的平衡因子的绝对值大于 1,则该二叉树是不平衡的。例如,如下图所示为不平衡二叉树。
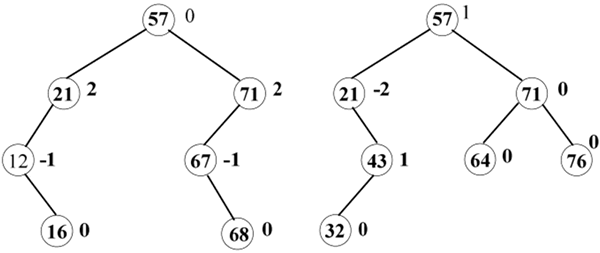
图 2 不平衡二叉树
若二叉排序树是平衡二叉树,则其平均查找长度与 logn 是同数量级的,可以尽量减少与关键字比较的次数。
构造平衡二叉排序树的过程如下图所示。
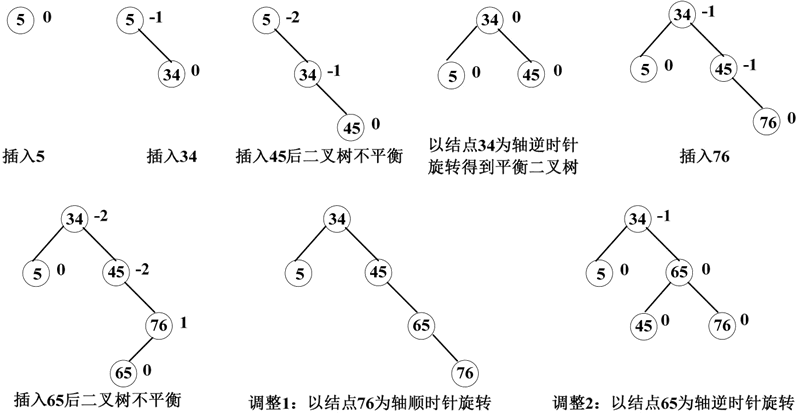
图 3 平衡二叉排序树的调整过程
初始时,二叉树是空树,因此是平衡二叉树。
一般情况下,新插入结点可能使二叉排序树失去平衡,通过使插入点最近的祖先结点恢复平衡,从而使上一层的祖先结点恢复平衡。
因此,为了使二叉排序树恢复平衡,需要从离插入点最近的结点开始调整。失去平衡的二叉排序树的类型及调整方法可以归纳为以下 4 种情形。
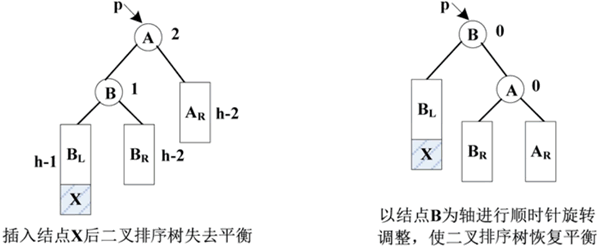
图 4 LL型二叉排序树的调整
距离插入点最近的失衡结点为 A,插入新结点 X 后,结点 A 的平衡因子由 1 变为 2,该二叉排序树失去平衡。
为了使二叉排序树恢复平衡且保持二叉排序树的性质不变,可以使结点 A 作为结点 B 的右子树,结点 B 的右子树作为结点 A 的左子树。这样就恢复了该二叉排序树的平衡,这相当于以结点 B 为轴,对结点 A 进行顺时针旋转。
为平衡二叉排序树的每个结点增加一个域 bf,用来表示对应结点的平衡因子,平衡二叉排序树的类型定义描述如下:
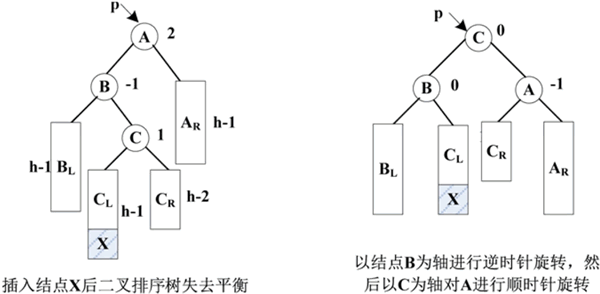
图 5 LR 型二叉排序树的调整
距离插入点最近的失衡结点为 A,在 C 的左子树 CL 下插入新结点 X 后,结点 A 的平衡因子由 1 变为 2,该二叉排序树失去平衡。
为了使二叉排序树恢复平衡且保持二叉排序树的性质不变,可以使:
这样就恢复了该二叉排序树的平衡。这相当于以结点 B 为轴,对结点 C 先做一次逆时针旋转,再以结点 C 为轴对结点 A 做一次顺时针旋转。
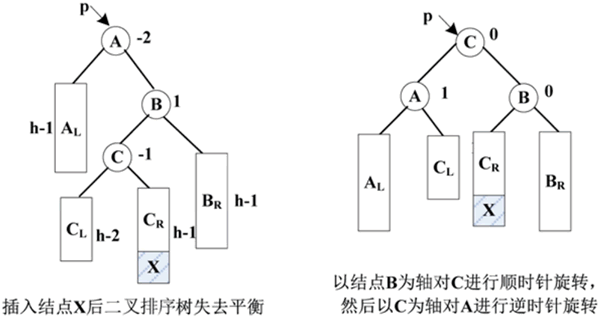
图 6 RL型二叉排序树的调整
距离插入点最近的失衡结点为 A,在 C 的右子树 CR 下插入新结点 X 后,结点 A 的平衡因子由 -1 变为 -2,该二叉排序树失去平衡。
为了使二叉排序树恢复平衡且保持二叉排序树的性质不变,可以使:
这样就恢复了该二叉排序树的平衡。这相当于以结点 B 为轴,对结点 C 先做一次顺时针旋转,再以结点 C 为轴对结点 A 做一次逆时针旋转。

图 7 RR型二叉排序树的调整
距离插入点最近的失衡结点为 A,在结点 B 的右子树 BR 下插入新结点 X 后,结点 A 的平衡因子由 -1 变为 -2,该二叉排序树失去平衡。
为了使二叉排序树恢复平衡且保持二叉排序树的性质不变,可以使:
这样就恢复了该二叉排序树的平衡。这相当于以结点 B 为轴,对结点 A 做一次逆时针旋转。
综合以上 4 种情况,在平衡二叉排序树中插入一个新结点 e 的算法描述如下:
平衡二叉树的定义
平衡二叉树也称为 AVL 树,平衡二叉树要么是一棵空二叉树,要么是具有以下性质的二叉树:- 平衡二叉树的左子树和右子树的深度之差的绝对值小于或等于 1;
- 左子树和右子树也是平衡二叉树。
若将二叉树中结点的平衡因子定义为结点的左子树与右子树之差,则平衡二叉树中每个结点的平衡因子的值只有 3 种可能:-1、0 和 1。
例如,如下图所示为平衡二叉树:

图 1 平衡二叉树
结点的右边表示平衡因子,因为该二叉树既是二叉排序树又是平衡树,因此该二叉树称为平衡二叉排序树。
若在二叉树中有一个结点的平衡因子的绝对值大于 1,则该二叉树是不平衡的。例如,如下图所示为不平衡二叉树。

图 2 不平衡二叉树
若二叉排序树是平衡二叉树,则其平均查找长度与 logn 是同数量级的,可以尽量减少与关键字比较的次数。
二叉排序树的平衡处理
在二叉排序树中插入一个新结点后,如何保证该二叉树是平衡二叉排序树呢?假设有一个关键字序列 {5,34,45,76,65},依照此关键字序列建立二叉排序树,且使该二叉排序树是平衡二叉排序树。构造平衡二叉排序树的过程如下图所示。

图 3 平衡二叉排序树的调整过程
初始时,二叉树是空树,因此是平衡二叉树。
- 在空二叉树中插入结点 5,该二叉树依然是平衡的。
- 当插入结点 34 后,该二叉树仍然是平衡的,结点 5 的平衡因子变为 -1。
- 当插入结点 45 后,结点 5 的平衡因子变为 -2,二叉树不平衡,需要进行调整。只需要以结点 34 为轴进行逆时针旋转,将二叉树变为以 34 为根,这时各个结点的平衡因子都为 0,二叉树即可转换为平衡二叉树。
- 继续插入结点 76,二叉树仍然是平衡的。
- 当插入结点 65 时,该二叉树失去平衡,如果仍然按照上述方法,仅以结点 45为轴进行旋转,就会失去二叉排序树的性质。既要保持二叉排序树的性质,又要保证该二叉树是平衡的,需要进行两次调整:先以结点 76 为轴进行顺时针旋转,再以结点 65 为轴进行逆时针旋转。
一般情况下,新插入结点可能使二叉排序树失去平衡,通过使插入点最近的祖先结点恢复平衡,从而使上一层的祖先结点恢复平衡。
因此,为了使二叉排序树恢复平衡,需要从离插入点最近的结点开始调整。失去平衡的二叉排序树的类型及调整方法可以归纳为以下 4 种情形。
1) LL型
LL型是指在离插入点最近的失衡结点的左子树的左子树中插入结点,导致二叉排序树失去平衡,如下图所示。
图 4 LL型二叉排序树的调整
距离插入点最近的失衡结点为 A,插入新结点 X 后,结点 A 的平衡因子由 1 变为 2,该二叉排序树失去平衡。
为了使二叉排序树恢复平衡且保持二叉排序树的性质不变,可以使结点 A 作为结点 B 的右子树,结点 B 的右子树作为结点 A 的左子树。这样就恢复了该二叉排序树的平衡,这相当于以结点 B 为轴,对结点 A 进行顺时针旋转。
为平衡二叉排序树的每个结点增加一个域 bf,用来表示对应结点的平衡因子,平衡二叉排序树的类型定义描述如下:
public class BSTNode { // 平衡二叉排序树的类型定义
{
int data;
int bf;
BTNode lchild, rchild;
static boolean taller; // 平衡化处理时判断高度是否增长
}
2) LR型
LR 型是指在离插入点最近的失衡结点的左子树的右子树中插入结点,导致二叉排序树失去平衡,如下图所示。
图 5 LR 型二叉排序树的调整
距离插入点最近的失衡结点为 A,在 C 的左子树 CL 下插入新结点 X 后,结点 A 的平衡因子由 1 变为 2,该二叉排序树失去平衡。
为了使二叉排序树恢复平衡且保持二叉排序树的性质不变,可以使:
- 结点 B 作为结点 C 的左子树;
- 结点 C 的左子树作为结点 B 的右子树;
- 将结点 C 作为新的根结点;
- 结点 A 作为 C 的右子树的根结点;
- 结点 C 的右子树作为 A 的左子树。
这样就恢复了该二叉排序树的平衡。这相当于以结点 B 为轴,对结点 C 先做一次逆时针旋转,再以结点 C 为轴对结点 A 做一次顺时针旋转。
3) RL型
RL 型是指在离插入点最近的失衡结点的右子树的左子树中插入结点,导致二叉排序树失去平衡,如下图所示。
图 6 RL型二叉排序树的调整
距离插入点最近的失衡结点为 A,在 C 的右子树 CR 下插入新结点 X 后,结点 A 的平衡因子由 -1 变为 -2,该二叉排序树失去平衡。
为了使二叉排序树恢复平衡且保持二叉排序树的性质不变,可以使:
- 结点 B 作为结点 C 的右子树;
- 结点 C 的右子树作为结点 B 的左子树;
- 将结点 C 作为新的根结点;
- 结点 A 作为 C 的右子树的根结点;
- 结点 C 的左子树作为 A 的右子树。
这样就恢复了该二叉排序树的平衡。这相当于以结点 B 为轴,对结点 C 先做一次顺时针旋转,再以结点 C 为轴对结点 A 做一次逆时针旋转。
4) RR型
RR 型是指在离插入点最近的失衡结点的右子树的右子树中插入结点,导致二叉排序树失去平衡,如下图所示。
图 7 RR型二叉排序树的调整
距离插入点最近的失衡结点为 A,在结点 B 的右子树 BR 下插入新结点 X 后,结点 A 的平衡因子由 -1 变为 -2,该二叉排序树失去平衡。
为了使二叉排序树恢复平衡且保持二叉排序树的性质不变,可以使:
- 结点 A 作为结点 B 的左子树的根结点;
- 结点 B 的左子树作为结点 A 的右子树。
这样就恢复了该二叉排序树的平衡。这相当于以结点 B 为轴,对结点 A 做一次逆时针旋转。
综合以上 4 种情况,在平衡二叉排序树中插入一个新结点 e 的算法描述如下:
- 若平衡二叉排序树是空树,则插入的新结点作为根结点,同时将该树的深度增加 1。
- 若二叉树中已经存在与结点 e 的关键字相等的结点,则不进行插入操作。
- 若结点 e 的关键字小于要插入位置的结点的关键字,则将 e 插入该结点的左子树,并将该结点的左子树高度增加 1,同时修改该结点的平衡因子;若该结点的平衡因子的绝对值大于 1,则需要进行平衡化处理。
- 若结点 e 的关键字大于要插入位置的结点的关键字,则将 e 插入该结点的右子树,并将该结点的右子树高度增加 1,同时修改该结点的平衡因子;若该结点的平衡因子的绝对值大于 1,则需要进行平衡化处理。
平衡二叉树的具体实现
二叉排序树的平衡处理算法实现包括 4 种情形:LL 型、LR 型、RL 型和 RR 型。其具体实现如下。1) LL型的平衡处理
对于 LL 型失去平衡的情形,只需要对离插入点最近的失衡结点进行一次顺时针旋转处理即可。其实现代码如下:
public void RightRotate(BSTNode p)
// 对以 p 为根的二叉排序树进行右旋转,处理之后 p 指向新的根结点,即旋转处理之前的左子树的根结点
{
BTNode lc = p.lchild; // lc 指向 p 的左子树的根结点
p.lchild = lc.rchild; // 将 lc 的右子树作为 p 的左子树
lc.rchild = p;
p.bf = 0;
lc.bf = 0;
p = lc; // p 指向新的根结点
}
2) LR型的平衡处理
对于 LR 型失去平衡的情形,需要进行两次旋转处理:先进行一次逆时针旋转,再进行一次顺时针旋转。其实现代码如下:
public void LeftBalance(BSTNode T)
// 对以 T 所指结点为根的二叉树进行左旋转平衡处理,并使 T 指向新的根结点
{
BTNode lc = T.lchild; // lc 指向 T 的左子树的根结点
switch(lc.bf) // 检查 T 的左子树的平衡度,并进行相应的平衡处理
{
case 1: // LL 型失衡处理。新结点插入 T 的左孩子的左子树上,需要进行单右旋处理
T.bf = lc.bf = 0;
RightRotate(T);
break;
case -1: // LR 型失衡处理。新结点插入 T 的左孩子的右子树上,需要进行双旋处理
BTNode rd = lc.rchild; // rd 指向 T 的左孩子的右子树的根结点
switch(rd.bf) // 修改 T 及其左孩子的平衡因子
{
case 1:
T.bf = -1;
lc.bf = 0;
break;
case 0:
T.bf = 0;
lc.bf = 0;
break;
case -1:
T.bf = 0;
lc.bf = 1;
break;
}
rd.bf = 0;
LeftRotate(T.lchild); // 对 T 的左子树进行左旋平衡处理
RightRotate(T); // 对 T 进行右旋平衡处理
}
}
3) RL型的平衡处理
对于 RL 型失去平衡的情形,需要进行两次旋转处理:先进行一次顺时针旋转,再进行一次逆时针旋转。其实现代码如下:
public void RightBalance(BSTNode T)
// 对以 T 所指结点为根的二叉树进行右旋转平衡处理,并使 T 指向新的根结点
{
BTNode rc = T.rchild; // rc 指向 T 的右子树的根结点
switch(rc.bf) // 检查 T 的右子树的平衡度,并进行相应的平衡处理
{
case -1: // 调用 RR 型平衡处理。新结点插入 T 的右孩子的右子树上,要进行单右旋处理
T.bf = 0;
rc.bf = 0;
LeftRotate(T);
break;
case 1: // RL 型平衡处理。新结点插入 T 的右孩子的左子树上,需要进行双旋处理
BTNode rd = rc.lchild; // rd 指向 T 的右孩子的左子树的根结点
switch(rd.bf) // 修改 T 及其右孩子的平衡因子
{
case -1:
T.bf = 1;
rc.bf = 0;
break;
case 0:
T.bf = 0;
rc.bf = 0;
break;
case 1:
T.bf = 0;
rc.bf = -1;
break;
}
rd.bf = 0;
RightRotate(T.rchild); // 对 T 的右子树进行右旋平衡处理
LeftRotate(T); // 对 T 进行左旋平衡处理
}
}
4) RR型的平衡处理
对于 RR 型失去平衡的情形,只需要对离插入点最近的失衡结点进行一次逆时针旋转处理即可。其实现代码如下:
public void LeftRotate(BSTNode p)
// 对以 p 为根的二叉排序树进行左旋,处理之后 p 指向新的根结点,即旋转处理之前的右子树的根结点
{
BTNode rc = p.rchild; // rc 指向 p 的右子树的根结点
p.rchild = rc.lchild; // 将 rc 的左子树作为 p 的右子树
rc.lchild = p;
p = rc; // p 指向新的根结点
}
平衡二叉排序树的查找过程与二叉排序树类似,其比较次数最多为树的深度,若树的结点个数为 n,则时间复杂度为 O(logn)。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: