快速排序算法,C语言快速排序算法详解
本节介绍一个非常优秀且最常用的排序算法,快速排序算法。这个算法极其重要,初学者一定要掌握。
快速排序尤其适用于对大数据的排序,它的高速和高效无愧于“快速”两个字。虽然说它是“最常用”的,可对于初学者而言,用它的人却非常少。因为虽然很快,但它也是逻辑最复杂、最难理解的算法,因为快速排序要用到递归和函数调用。
快速排序所采用的思想是分治的思想。所谓分治,就是指以一个数为基准,将序列中的其他数往它两边“扔”。以从小到大排序为例,比它小的都“扔”到它的左边,比它大的都“扔”到它的右边,然后左右两边再分别重复这个操作,不停地分,直至分到每一个分区的基准数的左边或者右边都只剩一个数为止。这时排序也就完成了。
所以快速排序的核心思想就是将小的往左“扔”,将大的往右“扔”,只要能实现这个,就与快速排序的思想吻合。从初学者的角度,“小的往左扔大的往右扔”首先能想到的往往是小的往前插,大的往后插。这确实是一个思路,但我们知道,数组是不擅长插入的。这种思路虽然能吻合快速排序的思想,但实现起来就不是“快速”排序,而是“慢速”排序了。所以这种方法是不可行的。于是就有了下面的“舞动算法”。
“舞动算法”的思想是用交换取代插入,大大提高了排序的速度。下面首先详细地讲解一下数组快速排序的过程。
假设序列中有 n 个数,将这 n 个数放到数组 A 中。“舞动算法”中一趟快速排序的算法是:
第一轮比较后序列就以 key 为中心分成了左右两部分,然后分别对左右两部分分别递归执行上面几个步骤,直到排序结束。
下面列举一个简单的例子,比如对如下数组 a 中的元素使用快速排序实现从小到大排序:
2) 然后定义 key 用于存放基准数,理论上该基准数可以取序列中的任何一个数。此处就取数组的第一个元素,即把 a[low] 赋给 key。
3) 然后 key 和 a[high] 比较,即 35 和 22 比较,35>22,则它们互换位置:
对于人类而言,这个过程确实比前面的排序算法复杂。但对于计算机而言,这个过程却没那么复杂。下面来写一个程序:
最终排序结果为:
-234 -70 -58 1 2 3 4 5 7 8 9 32 34 43 56 76 532 543 635 900 2500
这个程序就是按上面讲的过程写的。实际上还可以对这个程序进行优化。在快速排序算法中,每轮比较有且仅有一个 key 值,但是 key 值的位置是不断变化的,只有比较完一轮后 key 值的位置才固定。上面这个程序中每次执行 swap 时实际上交换的是 key 和 a[low] 或 key 和 a[high],而 key 的位置每次都是不一样的。所以既然 key 的位置是“动来动去”的,所以就不必将它赋到数组中了,等最后一轮比较结束后,它的位置“不动”了,再将它赋到数组中。
比如,数组 a 中元素为:3142。如果按从小到大排序,那么 key=3,按上面这个程序就是 3 和 2 互换。2 赋给 a[0] 是必需的,但 key 就没有必要赋给 a[3] 了。但你可以想象 key 是在 a[3] 这个位置,这个很重要。即此时序列变成 2142(key)。
然后 key 和 1 比较,不用换;key 和 4 比较,将 4 赋给 a[3],然后想象 key 在 4 的位置,即此时序列变成 214(key)4。此时 key 左边全是比 key 小的,key 的右边全是比 key 大的。这时 key 的位置就固定了,再将它赋到数组中,即 2134。
最终排序结果为:
-234 -70 -58 1 2 3 4 5 7 8 9 32 34 43 56 76 532 543 635 900 2500
快速排序实际上是冒泡排序的一种改进,是冒泡排序的升级版。这种改进就体现在根据分割序列的基准数,跨越式地进行交换。正是由于这种跨越式,使得元素每次移动的间距变大了,而不像冒泡排序那样一格一格地“爬”。快速排序是一次跨多格,所以总的移动次数就比冒泡排序少很多。
但是快速排序也有一个问题,就是递归深度的问题。调用函数要消耗资源,递归需要系统堆栈,所以递归的空间消耗要比非递归的空间消耗大很多。而且如果递归太深的话会导致堆栈溢出,系统会“撑”不住。快速排序递归的深度取决于基准数的选择,比如下面这个序列:
前面讲过,快速排序一般用于大数据排序,即数据的个数很多的时候(不是指数的值很大)。如果是小规模的排序,就用前面讲的几种简单排序方式就行了,不必使用快速排序。
插入排序通过将序列中的值插入一个已经排好序的序列中,直到该序列结束。插入排序是对冒泡排序的改进。它比冒泡排序快两倍。一般不用在数据的值大于 1000 的场合,或数据的个数超过 200 的序列。
选择排序在实际应用中处于与冒泡排序基本相同的地位。它们只是排序算法发展的初级阶段,在实际中使用较少。但是它们最好理解。
快速排序是大规模递归的算法,它比大部分排序算法都要快。一般用于数据个数比较多的情况。尽管可以在某些特殊的情况下写出比快速排序快的算法,但是就通常情况而言,没有比它更快的了。快速排序是递归的,对于内存非常有限的机器来说,它不是一个好的选择。
稳定性:假定在待排序的序列中存在多个相同的值,若经过排序后,这些值的相对次序保持不变,即在原序列中 ri=rj,且 ri 在 rj 之前,而在排序后的序列中 ri 仍在 rj 之前,则称这种排序算法是稳定的,否则称为不稳定的。
快速排序尤其适用于对大数据的排序,它的高速和高效无愧于“快速”两个字。虽然说它是“最常用”的,可对于初学者而言,用它的人却非常少。因为虽然很快,但它也是逻辑最复杂、最难理解的算法,因为快速排序要用到递归和函数调用。
快速排序所采用的思想是分治的思想。所谓分治,就是指以一个数为基准,将序列中的其他数往它两边“扔”。以从小到大排序为例,比它小的都“扔”到它的左边,比它大的都“扔”到它的右边,然后左右两边再分别重复这个操作,不停地分,直至分到每一个分区的基准数的左边或者右边都只剩一个数为止。这时排序也就完成了。
所以快速排序的核心思想就是将小的往左“扔”,将大的往右“扔”,只要能实现这个,就与快速排序的思想吻合。从初学者的角度,“小的往左扔大的往右扔”首先能想到的往往是小的往前插,大的往后插。这确实是一个思路,但我们知道,数组是不擅长插入的。这种思路虽然能吻合快速排序的思想,但实现起来就不是“快速”排序,而是“慢速”排序了。所以这种方法是不可行的。于是就有了下面的“舞动算法”。
“舞动算法”的思想是用交换取代插入,大大提高了排序的速度。下面首先详细地讲解一下数组快速排序的过程。
假设序列中有 n 个数,将这 n 个数放到数组 A 中。“舞动算法”中一趟快速排序的算法是:
- 设置两个变量 i、j,排序开始的时候:i=0,j=n–1。
- 以数组第一个元素为关键数据,赋给变量 key,即 key=A[0]。
- 从 j 开始向前搜索,即由后开始向前搜索(j--),找到第一个小于 key 的值 A[j],将 A[j] 和 A[i] 互换。
- 然后再从 i 开始向后搜索,即由前开始向后搜索(++i),找到第一个大于 key 的 A[i],将 A[i] 和 A[j] 互换。
- 重复第 3、4 步,直到 i=j。此时就能确保序列中所有元素都与 key 比较过了,且 key 的左边全部是比 key 小的,key 的右边全部是比 key 大的。
第一轮比较后序列就以 key 为中心分成了左右两部分,然后分别对左右两部分分别递归执行上面几个步骤,直到排序结束。
下面列举一个简单的例子,比如对如下数组 a 中的元素使用快速排序实现从小到大排序:
35 12 37 -58 54 76 22
1) 首先分别定义 low 和 high 用于存储数组第一个元素的下标和最后一个元素的下标,即 low=0,high=6。2) 然后定义 key 用于存放基准数,理论上该基准数可以取序列中的任何一个数。此处就取数组的第一个元素,即把 a[low] 赋给 key。
3) 然后 key 和 a[high] 比较,即 35 和 22 比较,35>22,则它们互换位置:
22 12 37 -58 54 76 35
4) 然后 low++==1,key 和 a[low] 比较,即 35 和 12 比较,12<35,则不用互换位置;继续 low++==2,然后 key 和 a[low] 比较,即 35 和 37 比较,37>35,则它们互换位置:22 12 35 -58 54 76 37
5) 然后 high--==5,key 和 a[high] 比较,即 35 和 76 比较,35<76,则不用互换位置;继续 high--==4,然后 key 和 a[high] 比较,即 35 和 54 比较,35<54,则不用互换位置;继续 high--==3,然后 key 和 a[high] 比较,即 35 和 -58 比较,35>–58,则它们互换位置:22 12 -58 35 54 76 37
6) 然后 low++==3,此时 low==high,第一轮比较结束。从最后得到的序列可以看出,35 左边的都比 35 小,35 右边的都比 35 大。这样就以 35 为中心,把原序列分成了左右两个部分。接下来只需要分别对左右两个部分分别重复上述操作就行了。对于人类而言,这个过程确实比前面的排序算法复杂。但对于计算机而言,这个过程却没那么复杂。下面来写一个程序:
# include <stdio.h>
void Swap(int *, int *); //函数声明, 交换两个变量的值
void QuickSort(int *, int, int); //函数声明, 快速排序
int main(void)
{
int i; //循环变量
int a[] = {900, 2, -58, 3, 34, 5, 76, 7, 32, 4, 43, 9, 1, 56, 8,-70, 635, -234, 532, 543, 2500};
QuickSort(a, 0, 20); /*引用起来很简单, 0为第一个元素的下标, 20为最后一个元素的下标*/
printf("最终排序结果为:\n");
for (i=0; i<21; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
void Swap(int *p, int *q)
{
int buf;
buf = *p;
*p = *q;
*q = buf;
return;
}
void QuickSort(int *a, int low, int high)
{
int i = low;
int j = high;
int key = a[low];
if (low >= high) //如果low >= high说明排序结束了
{
return ;
}
while (low < high) //该while循环结束一次表示比较了一轮
{
while (low < high && key <= a[high])
{
--high; //向前寻找
}
if (key > a[high])
{
Swap(&a[low], &a[high]);
++low;
}
while (low < high && key >= a[low])
{
++low; //向后寻找
}
if (key < a[low])
{
Swap(&a[low], &a[high]);
--high;
}
}
QuickSort(a, i, low-1); //用同样的方式对分出来的左边的部分进行同上的做法
QuickSort(a, low+1, j); //用同样的方式对分出来的右边的部分进行同上的做法
}
输出结果是:最终排序结果为:
-234 -70 -58 1 2 3 4 5 7 8 9 32 34 43 56 76 532 543 635 900 2500
这个程序就是按上面讲的过程写的。实际上还可以对这个程序进行优化。在快速排序算法中,每轮比较有且仅有一个 key 值,但是 key 值的位置是不断变化的,只有比较完一轮后 key 值的位置才固定。上面这个程序中每次执行 swap 时实际上交换的是 key 和 a[low] 或 key 和 a[high],而 key 的位置每次都是不一样的。所以既然 key 的位置是“动来动去”的,所以就不必将它赋到数组中了,等最后一轮比较结束后,它的位置“不动”了,再将它赋到数组中。
比如,数组 a 中元素为:3142。如果按从小到大排序,那么 key=3,按上面这个程序就是 3 和 2 互换。2 赋给 a[0] 是必需的,但 key 就没有必要赋给 a[3] 了。但你可以想象 key 是在 a[3] 这个位置,这个很重要。即此时序列变成 2142(key)。
然后 key 和 1 比较,不用换;key 和 4 比较,将 4 赋给 a[3],然后想象 key 在 4 的位置,即此时序列变成 214(key)4。此时 key 左边全是比 key 小的,key 的右边全是比 key 大的。这时 key 的位置就固定了,再将它赋到数组中,即 2134。
# include <stdio.h>
void QuickSort(int *, int, int); /*现在只需要定义一个函数, 不用交换还省了一个函数, 减少了代码量*/
int main(void)
{
int i; //循环变量
int a[] = {900, 2, -58, 3, 34, 5, 76, 7, 32, 4, 43, 9, 1, 56, 8,-70, 635, -234, 532, 543, 2500};
QuickSort(a, 0, 20); /*引用起来很简单, 0为第一个元素的下标, 20为最后一个元素的下标*/
printf("最终排序结果为:\n");
for (i=0; i<21; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
void QuickSort(int *a, int low, int high)
{
int i = low;
int j = high;
int key = a[low];
if (low >= high) //如果low >= high说明排序结束了
{
return ;
}
while (low < high) //该while循环结束一次表示比较了一轮
{
while (low < high && key <= a[high])
{
--high; //向前寻找
}
if (key > a[high])
{
a[low] = a[high]; //直接赋值, 不用交换
++low;
}
while (low < high && key >= a[low])
{
++low; //向后寻找
}
if (key < a[low])
{
a[high] = a[low]; //直接赋值, 不用交换
--high;
}
}
a[low] = key; //查找完一轮后key值归位, 不用比较一次就互换一次。此时key值将序列分成左右两部分
QuickSort(a, i, low-1); //用同样的方式对分出来的左边的部分进行同上的做法
QuickSort(a, low+1, j); //用同样的方式对分出来的右边的部分进行同上的做法
}
输出结果是:最终排序结果为:
-234 -70 -58 1 2 3 4 5 7 8 9 32 34 43 56 76 532 543 635 900 2500
总结
快速排序的基本思想是通过一趟快速排序,将要排序的数据分割成独立的两部分,其中一部分的所有数据比另外一部分的所有数据都要小,然后再按此方法递归地对这两部分数据分别进行快速排序。如此一直进行下去,直到排序完成。快速排序实际上是冒泡排序的一种改进,是冒泡排序的升级版。这种改进就体现在根据分割序列的基准数,跨越式地进行交换。正是由于这种跨越式,使得元素每次移动的间距变大了,而不像冒泡排序那样一格一格地“爬”。快速排序是一次跨多格,所以总的移动次数就比冒泡排序少很多。
但是快速排序也有一个问题,就是递归深度的问题。调用函数要消耗资源,递归需要系统堆栈,所以递归的空间消耗要比非递归的空间消耗大很多。而且如果递归太深的话会导致堆栈溢出,系统会“撑”不住。快速排序递归的深度取决于基准数的选择,比如下面这个序列:
5 1 9 3 7 4 8 6 2
5 正好处于 1~9 的中间,选择 5 作基准数可以平衡两边的递归深度。可如果是:1 5 9 3 7 4 8 6 2
选择 1 作为基准数,那么递归深度就全部都加到右边了。如果右边有几万个数的话则系统直接就崩溃了。所以需要对递归深度进行优化。怎么优化呢?就是任意取三个数,一般是取序列的第一个数、中间数和最后一个数,然后选择这三个数中大小排在中间的那个数作为基准数,这样起码能确保获取的基准数不是两个极端。前面讲过,快速排序一般用于大数据排序,即数据的个数很多的时候(不是指数的值很大)。如果是小规模的排序,就用前面讲的几种简单排序方式就行了,不必使用快速排序。
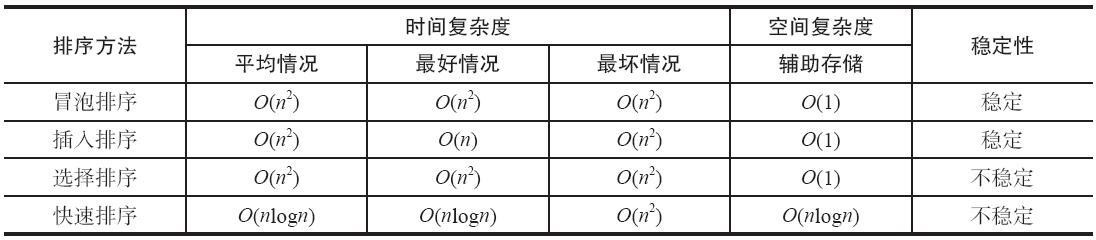
四种排序算法的比较
冒泡排序是最慢的排序算法。在实际运用中它是效率最低的算法。它通过一趟又一趟地比较数组中的每一个元素,使较大的数据下沉,较小的数据上升。插入排序通过将序列中的值插入一个已经排好序的序列中,直到该序列结束。插入排序是对冒泡排序的改进。它比冒泡排序快两倍。一般不用在数据的值大于 1000 的场合,或数据的个数超过 200 的序列。
选择排序在实际应用中处于与冒泡排序基本相同的地位。它们只是排序算法发展的初级阶段,在实际中使用较少。但是它们最好理解。
快速排序是大规模递归的算法,它比大部分排序算法都要快。一般用于数据个数比较多的情况。尽管可以在某些特殊的情况下写出比快速排序快的算法,但是就通常情况而言,没有比它更快的了。快速排序是递归的,对于内存非常有限的机器来说,它不是一个好的选择。

 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: