过拟合和欠拟合到底是什么(非常详细)
机器学习中一个重要的话题便是模型的泛化能力。泛化能力强的模型才是好模型。
对于训练好的模型,若在训练集表现差,在测试集表现同样会很差,这可能是欠拟合导致的。欠拟合是指模型拟合程度不高,数据距离拟合曲线较远,或指模型没有很好地捕捉到数据特征,不能很好地拟合数据。
为了防止模型从训练数据中记住错误或无关紧要的模式,最优解决方法是获取更多的训练数据。模型的训练数据越多,泛化能力自然也越好。
如果无法获取更多数据,次优解决方法是调节模型允许存储的信息量,或对模型允许存储的信息加以约束。如果一个网络只能记住几个模式,那么优化过程会迫使模型集中学习最重要的模式,这样更可能得到良好的泛化。
在深度学习中,模型可学习参数的个数通常被称为模型的容量(capacity)。直观上来看,参数更多的模型拥有更大的记忆容量(memorization capacity),因此能够在训练样本和目标之间轻松地学会完美的字典式映射,这种映射没有任何泛化能力。
例如,拥有 500 000 个二进制参数的模型,能够轻松学会 MNIST 训练集中所有数字对应的类别——只需让 50 000 个数字每个都对应 10 个二进制参数。但这种模型对于新数字样本的分类毫无用处。
与此相反,如果网络的记忆资源有限,则无法轻松学会这种映射。因此,为了让损失最小化,网络必须学会对目标具有很强的预测能力的压缩表示,这也正是我们感兴趣的数据表示。
需要记住的是,使用的模型应该具有足够多的参数,以防欠拟合,即模型应避免记忆资源不足。在容量过大与容量不足之间要找到一个折中。要找到合适的模型大小,一般的工作流程是开始时选择相对较少的层和参数,然后逐渐增加层的大小或增加新层,直到这种增加对验证损失的影响变得很小。
例如,在电影评价上尝试减小网络大小:
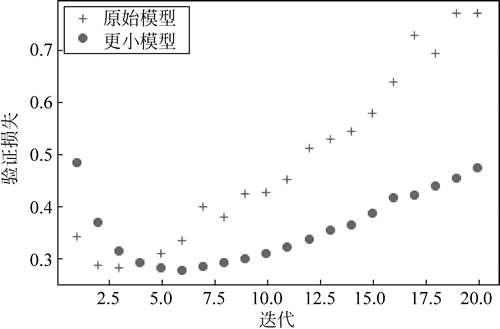
图 1 换用更小的网络验证损失效果
由图 1 可见,更小的网络开始过拟合的时间要易于参考网络(前者 6 轮后开始过拟合,而后者 4 轮后开始过拟合),且开始过拟合后,它的速度也更慢。
下面再向这个基准中添加一个容量更大的网络(容量远大于问题所需)。
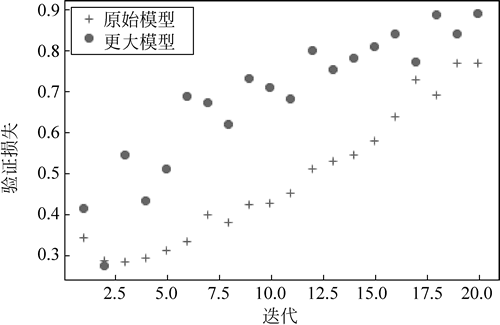
图 2 换用更大的网络验证损失效果
从图 2 中可以看出,更大的网络只过了一轮就开始过拟合,过拟合也更严重。其验证损失的波动也更大。
下图同时给出了更小和更大这两个网络的训练损失:

图 3 同时对比更小和更大网络的训练损失效果
从图 3 中可见,更大网络的训练损失很快就接近于零。网络的容量越大,它拟合训练数据(即得到很小的训练损失)的速度就越快,但也更容易过拟合(导致训练损失和验证损失有很大差异)。
这个成本有两种形式。
在 Keras 中,添加权重正则化的方法是向层传递权重正则化项实例(weight regularizer instance)作为关键字参数。
例如,将向电影评论分类网络中添加 L2 权重正则化:
下图显示了 L2 正则化惩罚的影响:

图 4 L2正则化对验证损失的影响
如图 4 所示,即使两个模型的参数个数相同,具有 L2 正则化的模型(圆点)比原始模型(十字)更不容易过拟合。
还可以用 Keras 中以下这些权重正则化项来代替 L2 正则化:
假设在训练过程中,某一层对给定输入样本的返回值应该是向量(0.2,0.5,1.3,0.8,1.1),使用 dropout 后,这个向量会有几个随机的元素变成 0,如(0,0.5,1.3,0,1.1),dropout 比率(dropout rate)是被设为 0 的特征所占的比例,通常在 0.2~0.5 范围内。测试时没有单元被舍弃,而该层的输出值需要按 dropout 比率缩小,因为这时比训练时有更多的单元被激活,需要加以平衡。
假设有一个包含某层输出的 NumPy 矩阵 layer_output,其形状为 [batch_size,features],训练时,随机将矩阵中一部分值设为 0:
测试时,将输出按 dropout 比率缩小。此处乘以 0.5(前面舍弃了一半的单元)。
注意,为了实现这一过程,还可以让两个运算都在训练时进行,而测试时输出保持不变。这通常也是实践中的实现方式:
在 Keras 中,可以通过 dropout 层向网络中引入 dropout,dropout 将被应用于前面一层的输出:
向 IMDB 网络中添加两个 dropout 层,观察它们降低过拟合的效果:
下图给出了结果的图示,再次看到,这种方法的性能相比原始模型有明显提高。
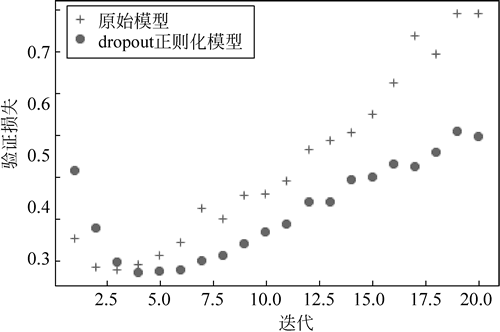
图 5 dropout对验证损失的影响
因此,可总结防止神经网络过拟合的常用方法主要有:
对于训练好的模型,若在训练集表现差,在测试集表现同样会很差,这可能是欠拟合导致的。欠拟合是指模型拟合程度不高,数据距离拟合曲线较远,或指模型没有很好地捕捉到数据特征,不能很好地拟合数据。
为了防止模型从训练数据中记住错误或无关紧要的模式,最优解决方法是获取更多的训练数据。模型的训练数据越多,泛化能力自然也越好。
如果无法获取更多数据,次优解决方法是调节模型允许存储的信息量,或对模型允许存储的信息加以约束。如果一个网络只能记住几个模式,那么优化过程会迫使模型集中学习最重要的模式,这样更可能得到良好的泛化。
减小网络大小
防止过拟合的最简单的方法就是减小模型大小,即减小模型中可学习参数的个数(这由层数和每层的单元个数决定)。在深度学习中,模型可学习参数的个数通常被称为模型的容量(capacity)。直观上来看,参数更多的模型拥有更大的记忆容量(memorization capacity),因此能够在训练样本和目标之间轻松地学会完美的字典式映射,这种映射没有任何泛化能力。
例如,拥有 500 000 个二进制参数的模型,能够轻松学会 MNIST 训练集中所有数字对应的类别——只需让 50 000 个数字每个都对应 10 个二进制参数。但这种模型对于新数字样本的分类毫无用处。
与此相反,如果网络的记忆资源有限,则无法轻松学会这种映射。因此,为了让损失最小化,网络必须学会对目标具有很强的预测能力的压缩表示,这也正是我们感兴趣的数据表示。
需要记住的是,使用的模型应该具有足够多的参数,以防欠拟合,即模型应避免记忆资源不足。在容量过大与容量不足之间要找到一个折中。要找到合适的模型大小,一般的工作流程是开始时选择相对较少的层和参数,然后逐渐增加层的大小或增加新层,直到这种增加对验证损失的影响变得很小。
例如,在电影评价上尝试减小网络大小:
from keras.datasets import imdb import numpy as np '''原始模型''' from keras import models from keras import layers original_model=models.Sequential() original_model.add(layers.Dense(16,activation='relu',input_shape=(10000,))) original_model.add(layers.Dense(16,activation='relu')) original_model.add(layers.Dense(1,activation='sigmoid')) '''容量更小的模型''' smaller_model=models.Sequential() smaller_model.add(layers.Dense(4,activation='relu',input_shape=(10000,))) smaller_model.add(layers.Dense(4,activation='relu')) smaller_model.add(layers.Dense(1,activation='sigmoid')) smaller_model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])下图比较了原始网络与更小网络的验证损失。圆点表示更小网络的验证损失值,十字表示原始网络的验证损失值。

图 1 换用更小的网络验证损失效果
由图 1 可见,更小的网络开始过拟合的时间要易于参考网络(前者 6 轮后开始过拟合,而后者 4 轮后开始过拟合),且开始过拟合后,它的速度也更慢。
下面再向这个基准中添加一个容量更大的网络(容量远大于问题所需)。
bigger_model=models.Sequential() bigger_model.add(layers.Dense(512,activation='relu',input_shape=(10000,))) bigger_model.add(layers.Dense(512,activation='relu')) bigger_model.add(layers.Dense(1,activation='sigmoid'))下图显示了更大的网络与参考网络的性能对比。圆点表示更大网络的验证损失值,十字表示原始网络的验证损失值。

图 2 换用更大的网络验证损失效果
从图 2 中可以看出,更大的网络只过了一轮就开始过拟合,过拟合也更严重。其验证损失的波动也更大。
下图同时给出了更小和更大这两个网络的训练损失:

图 3 同时对比更小和更大网络的训练损失效果
从图 3 中可见,更大网络的训练损失很快就接近于零。网络的容量越大,它拟合训练数据(即得到很小的训练损失)的速度就越快,但也更容易过拟合(导致训练损失和验证损失有很大差异)。
添加权重正则化
一种常见的降低过拟合的方法就是强制让模型权重只能取较小的值,从而限制模型的复杂度,这使得权重值的分布更加规则(regular),这种方法叫作权重正则化(weight regularization),其实现方法是向网络损失函数中添加与较大权重值相关的成本(cost)。这个成本有两种形式。
- L1 正则化(L1 regularization):添加的成本与权重系数的绝对值(权重的 L1 范数(norm))成正比。
- L2 正则化(L2 regularization):添加的成本与权重系数的平方(权重的 L2 范数)成正比。神经网络的 L2 正则化也叫权重衰减(weight decay)。权重衰减与 L2 正则化在数学上是完全相同的。
在 Keras 中,添加权重正则化的方法是向层传递权重正则化项实例(weight regularizer instance)作为关键字参数。
例如,将向电影评论分类网络中添加 L2 权重正则化:
'''向模型添加L2权重正则化''' from keras import regularizers l2_model=models.Sequential() l2_model.add(layers.Dense(16,kernel_regularizer=regularizers.l2(0.001),activation='relu',input_shape=(10000,))) l2_model.add(layers.Dense(16,kernel_regularizer=regularizers.l2(0.001),activation='relu')) l2_model.add(layers.Dense(1,activation='sigmoid'))l2(0.001)的作用为该层权重矩阵的每个系数都会使网络总损失增加 0.001×weight_coefficient_value。注意,因为这个惩罚项只在训练时添加,所以这个网络的训练损失会比测试损失大很多。
下图显示了 L2 正则化惩罚的影响:

图 4 L2正则化对验证损失的影响
如图 4 所示,即使两个模型的参数个数相同,具有 L2 正则化的模型(圆点)比原始模型(十字)更不容易过拟合。
还可以用 Keras 中以下这些权重正则化项来代替 L2 正则化:
from keras import regularizers #L1正则化 regularizers.l1(0.001) #同时进行L1与L2正则化 regularizers.l1_l2(l1=0.001,l2=0.001)
添加dropout正则化
dropout 是神经网络中最有效也最常用的正则化方法之一。对某一层使用 doupout,就是在训练过程中随机将该层的一些输出特征舍弃(设置为 0)。假设在训练过程中,某一层对给定输入样本的返回值应该是向量(0.2,0.5,1.3,0.8,1.1),使用 dropout 后,这个向量会有几个随机的元素变成 0,如(0,0.5,1.3,0,1.1),dropout 比率(dropout rate)是被设为 0 的特征所占的比例,通常在 0.2~0.5 范围内。测试时没有单元被舍弃,而该层的输出值需要按 dropout 比率缩小,因为这时比训练时有更多的单元被激活,需要加以平衡。
假设有一个包含某层输出的 NumPy 矩阵 layer_output,其形状为 [batch_size,features],训练时,随机将矩阵中一部分值设为 0:
#训练时,舍弃50%的输出单元 layer_output * =np.randint(0, high=2, size=layer_output.shape)
测试时,将输出按 dropout 比率缩小。此处乘以 0.5(前面舍弃了一半的单元)。
#测试时 ayer_output * =0.5
注意,为了实现这一过程,还可以让两个运算都在训练时进行,而测试时输出保持不变。这通常也是实践中的实现方式:
#训练时 layer_output * =np.randint(0, high=2, size=layer_output.shape) #注意,是成比例放大而不是成比例缩小 layer_output/=0.5
在 Keras 中,可以通过 dropout 层向网络中引入 dropout,dropout 将被应用于前面一层的输出:
model.add(layers.Dropout(0.5))
向 IMDB 网络中添加两个 dropout 层,观察它们降低过拟合的效果:
dpt_model=models.Sequential() dpt_model.add(layers.Dense(16,activation='relu',input_shape=(10000,))) dpt_model.add(layers.Dropout(0.5)) dpt_model.add(layers.Dense(16,activation='relu')) dpt_model.add(layers.Dropout(0.5)) dpt_model.add(layers.Dense(1,activation='sigmoid'))
下图给出了结果的图示,再次看到,这种方法的性能相比原始模型有明显提高。

图 5 dropout对验证损失的影响
因此,可总结防止神经网络过拟合的常用方法主要有:
- 获取更多的训练数据;
- 减小网络容量;
- 添加权重正则化;
- 添加dropout。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: